Heat and Thermodynamics 5 Question 32
33. One mole of a monatomic ideal gas is taken through a cycle $A B C D A$ as shown in the $p-V$ diagram. Column II gives the characteristics involved in the cycle. Match them with each of the processes given in Column I.
(2011)
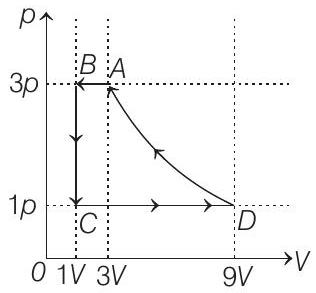
| Column I | Column II | ||
|---|---|---|---|
| (A) | Process $A \rightarrow B$ | (p) | Internal energy decreases |
| (B) | Process $B \rightarrow C$ | (q) | Internal energy increases |
| (C) | Process $C \rightarrow D$ | (r) | Heat is lost |
| (D) | Process $D \rightarrow A$ | (s) | Heat is gained |
| (t) | Work is done on the gas |
Show Answer
Answer:
Correct Answer: 33. (A) $\rightarrow$ p, r, t; (B) $\rightarrow$ p, r; (C) $\rightarrow$ q, s; (D) $\rightarrow$ r, t
Solution:
- Internal energy $\propto T \propto p V$
This is because $U=\frac{n f}{2} R T=\frac{f}{2}(p V)$
Here, $n=$ number of moles, $f=$ degree of freedom.
$\therefore$ If the product $p V$ increases then internal energy will increase and if product decreases the internal energy will decrease.
Further, work is done on the gas, if volume of gas decreases. For heat exchange,
$$ Q=W+\Delta U $$
Work done is area under $p-V$ graph. If volume increases work done by gas is positive and if volume decreases work done by gas is negative. Further $\Delta U$ is positive if product of $p V$ is increasing and $\Delta U$ is negative if product of $p V$ is decreasing.
If heat is taken by the gas $Q$ is positive and if heat is lost by the gas $Q$ is negative. Keeping the above points in mind the answer to this question is as under.
(A) $\rightarrow(p, r, t)$;
(B) $\rightarrow(p, r)$; $(C) \rightarrow(q, s) ;(D) \rightarrow(r, t)$






