Heat and Thermodynamics 5 Question 2
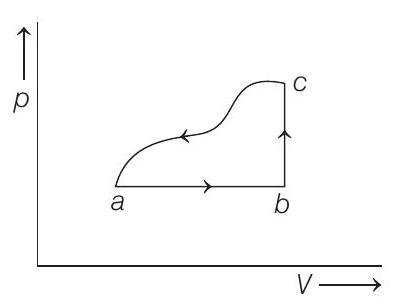
2. A sample of an ideal gas is taken through the cyclic process $a b c a$ as shown in the figure. The change in the internal energy of the gas along the path $c a$ is $-180 J$. The gas absorbs $250 J$ of heat along the path $a b$ and $60 J$ along the path $b c$. The work done by the gas along the path $a b c$ is
(2019 Main, 12 April I)
(a) $120 J$
(b) $130 J$
(c) $100 J$
(d) $140 J$
Show Answer
Solution:
- Key Idea In $p-V$ curve, work done $d W$, change in internal energy $\Delta U$ and heat absorbed $\Delta Q$ are connected with first law of thermodynamics, i.e.
$$ \Delta Q=\Delta U+d W $$
and total change in internal energy in complete cycle is always zero. Using this equation in different part of the curve, we can solve the
given problem.
In Process $a \rightarrow b$
$$ \begin{aligned} \text { Given, } & & \Delta Q _{a b} & =250 J \\ & \therefore & 250 J & =\Delta U _{a b}+d W _{a b} \end{aligned} $$
In Process $b \rightarrow c$
$$ \text { Given, } \quad \Delta Q _{b c}=60 J $$
Also, $V$ is constant, so $d V=0$
$$ \begin{array}{rlrl} \Rightarrow & d W _{b c} & =p(d V) _{b c}=0 \\ & \therefore & 60 J & =\Delta U _{b c}+0 \\ \Rightarrow & & \Delta U _{b c} & =60 J \end{array} $$
In Process $c \rightarrow a$
Given, $\quad \Delta U _{c a}=-180 J$
Now, for complete cycle,
$$ \Delta U _{a b c a}=\Delta U _{a b}+\Delta U _{b c}+\Delta U _{c a}=0 $$
From Eqs. (iii), (iv) and (v), we get
$$ \begin{aligned} \Delta U _{a b} & =-\Delta U _{b c}-\Delta U _{c a} \\ \Delta U _{a b} & =-60+180=120 J \end{aligned} $$
From Eq. (ii), we get
$$ \begin{array}{rlrl} & & 250 J & =120 J+d W _{a b} \\ \Rightarrow \quad & d W _{a b} & =130 J \end{array} $$
From Eqs. (i) and (vii), we get
Work done by the gas along the path $a b c$,
$$ \begin{aligned} d W _{a b c} & =d W _{a b}+d W _{b c} \\ & =130 J+0 K \\ \Rightarrow \quad d W _{a b c} & =130 J \end{aligned} $$
