SATHEE: Heat and Thermodynamics 5 Question 11

Heat and Thermodynamics 5 Question 11

11. Three Carnot engines operate in series between a heat source at a temperature $T _1$ and a heat sink at temperature $T _4$ (see figure). There are two other reservoirs at temperatures $T _2$ and $T _3$, as shown with $T _1>T _2>T _3>T _4$. The three engines are equally efficient if

(Main 2019, 10 Jan I)

(a) $T _2=\left(T _1^{3} T _4\right)^{1 / 4} ; T _3=\left(T _1 T _4^{3}\right)^{1 / 4}$

(b) $T _2=\left(T _1^{2} T _4\right)^{1 / 3} ; T _3=\left(T _1 T _4^{2}\right)^{1 / 3}$

(d) $T _2=\left(T _1 T _4^{2}\right)^{1 / 3} ; T _3=\left(T _1^{2} T _4\right)^{1 / 3}$

Show Answer

Solution:

Given, Carnot engines operates as,

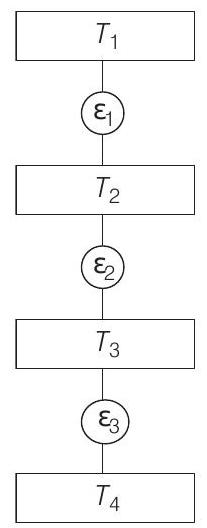
As, efficiency of a Carnot’s engine is given by

We have,

$$ \eta=1-\frac{T _{\text {sink }}}{T _{\text {source }}} $$

$\eta _1=$ efficiency of engine $\varepsilon _1=1-\frac{T _2}{T _1}$

$\eta _2=$ efficiency of engine $\varepsilon _2=1-\frac{T _3}{T _2}$ $\eta _3=$ efficiency of engine $\varepsilon _3=1-\frac{T _4}{T _3}$

For equal efficiencies,

$$ \begin{array}{rlrl} & \eta _1=\eta _2=\eta _3 \\ \Rightarrow \quad 1-\frac{T _2}{T _1} & =1-\frac{T _3}{T _2}=1-\frac{T _4}{T _3} \\ \Rightarrow \quad & \frac{T _2}{T _1} & =\frac{T _3}{T _2}=\frac{T _4}{T _3} \\ \Rightarrow \quad & T _2^{2} & =T _1 T _3 \text { and } T _3^{2}=T _2 T _4 \\ \Rightarrow \quad T _2^{4} & =T _1^{2} T _3^{2} \\ & & T _2^{4} & =T _1^{2} T _2 T _4 \\ \text { or } & T _2^{3} & =T _4 T _1^{2} \\ \text { Also, } & T _2 & =\left(T _1^{2} T _4\right)^{\frac{1}{3}} \\ & & T _3^{4} & =T _2^{2} T _4^{2}=T _1 T _3 T _4^{2} \\ & & T _3^{3} & =T _1 T _4^{2} \text { or } T _3=\left(T _1 T _4^{2}\right)^{\frac{1}{3}} \end{array} $$

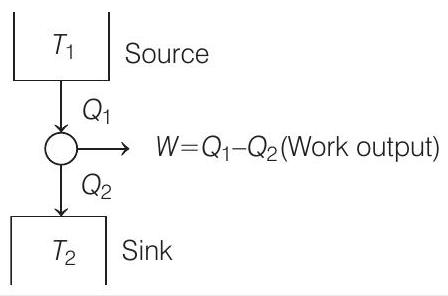
Key idea In a Carnot engine the heat flow from higher temperature source $\left(\right.$ at $\left.T _1\right)$ to lower temperature $\operatorname{sink}\left(a t T _2\right)$ and give the work done equal to the $W=Q _1-Q _2$.

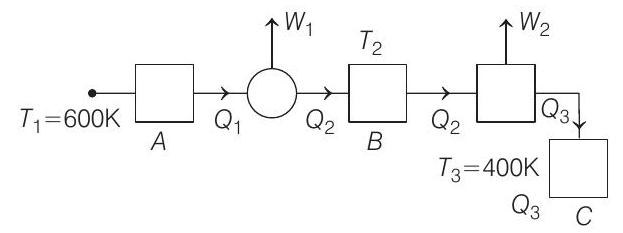
For the given condition, Carnot engine $A$ and $B$ are operated in series as shown below

where,

$Q _1=$ heat rejected by engine $A$ at $T _1 K$,

$Q _2=$ heat received by engine $B$ at $T _2 K$ and

$Q _3=$ heat rejected by engine $B$ to source $C$ at $T _3 K$.

According to Carnot engine principle,

$W _1=Q _1-Q _2$ (work-output from source $A$ and $B$ )

$W _2=Q _2-Q _3$ (work output from source $B$ and $C$ )

As per the given condition, if the work outputs of the two engines are equal, then

$$ \Rightarrow \quad \begin{aligned} & Q _1-Q _2=Q _2-Q _3 \\ & \Rightarrow \quad \\ & Q _1+Q _3=2 Q _2 \end{aligned} $$

$$ \begin{aligned} & & \frac{Q _1}{Q _2}+\frac{Q _3}{Q _2}=2 \\ \text { Therefore } & & \frac{T _1}{T _2}+\frac{T _3}{T _2}=2 \\ \text { So, } & & \frac{T _1+T _3}{T _2}=2 \\ \Rightarrow \quad & T _2 & =\frac{T _1+T _3}{2}=\frac{600+400}{2} \\ & T _2 & =500 K \end{aligned} $$

पिछला

अगला