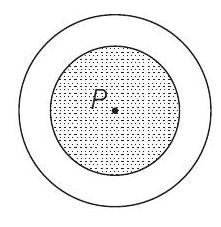
Heat and Thermodynamics 3 Question 32
32. A point source of heat of power
(1991, 1M)
Show Answer
Solution:
- Thermal resistance
Equating this rate with the power of the source.
or thickness