Heat and Thermodynamics 3 Question 3
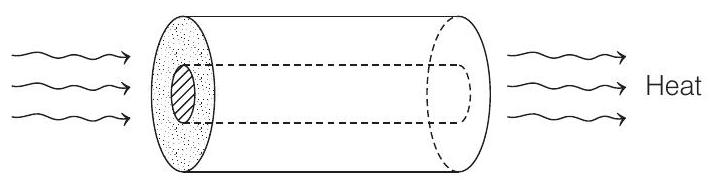
3. A cylinder of radius $R$ is surrounded by a cylindrical shell of inner radius $R$ and outer radius $2 R$. The thermal conductivity of the material of the inner cylinder is $K _1$ and that of the outer cylinder is $K _2$. Assuming no loss of heat, the effective
thermal conductivity of the system for heat flowing along the length of the cylinder is
(a) $\frac{K _1+K _2}{2}$
(b) $\frac{K _1+3 K _2}{4}$
(c) $\frac{2 K _1+3 K _2}{5}$
(d) $K _1+K _2$
(2019 Main, 12 Jan I)
Show Answer
Solution:
- Both the given cylinders are in parallel as heat flow is given along length. In parallel, equivalent thermal conductivity of system is
$$ K _{eq}=\frac{K _1 A _1+K _2 A _2}{A _1+A _2} $$
So, in given system
$K _{\text {eq }}=\frac{K _1\left(\pi R^{2}\right)+K _2\left[\pi(2 R)^{2}-\pi R^{2}\right]}{\left(\pi R^{2}\right)+\left(4 \pi R^{2}-\pi R^{2}\right)}$ or $K _{\text {eq }}=\frac{K _1+3 K _2}{4}$
