Heat and Thermodynamics 2 Question 8
11. The apparatus shown in figure consists of four glass columns connected by horizontal sections. The height of two central columns
Show Answer
Solution:
- Density of a liquid varies with temperature as
Here,
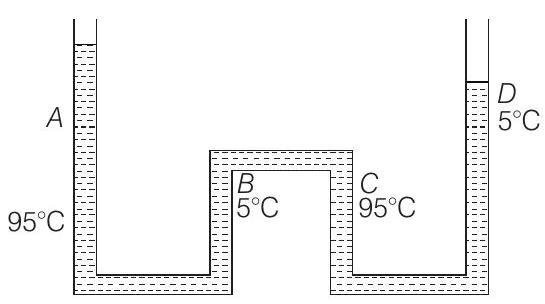
In the figure
Now, pressure at
Solving this equation, we get






