Heat and Thermodynamics 2 Question 3
6. The ends $Q$ and $R$ of two thin wires, $P Q$ and $R S$, are soldered (joined) together. Initially, each of the wire has a length of $1 m 10^{\circ} C$. Now, the end $P$ is maintained at $10^{\circ} C$, while the end $S$ is heated and maintained at $400^{\circ} C$. The system is thermally insulated from its surroundings. If the thermal conductivity of wire $P Q$ is twice that of the wire $R S$ and the coefficient of linear thermal expansion of $P Q$ is $1.2 \times 10^{-5} K$ ${ }^{-1}$, the change in length of the wire $P Q$ is
(2016 Adv.)
(a) $0.78 mm$
(b) $0.90 mm$
(c) $1.56 mm$
(d) $2.34 mm$
Show Answer
Answer:
Correct Answer: 6. (a)
Solution:
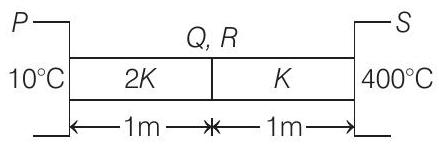
Rate of heat flow from $P$ to $Q$
$$ \frac{d Q}{d t}=\frac{2 K A(T-10)}{1} $$
Rate of heat flow from $Q$ to $S$
$$ \frac{d Q}{d t}=\frac{K A(4000-T)}{1} $$
At steady state rate of heat flow is same
$\therefore \frac{2 K A(T-10)}{1}=K A(400-T)$
or $2 T-20=400-T$ or $3 T=420$
$\therefore \quad T=140^{\circ}$
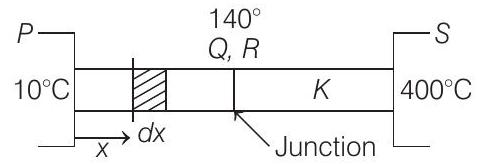
Temperature of junction is $140^{\circ} C$
Temperature at a distance $x$ from end $P$
is $T _x=\left(130 x+10^{\circ}\right)$
Change in length $d x$ is suppose $d y$
Then, $d y=\alpha d x\left(T _x-10\right)$
$$ \begin{aligned} \int _0^{\Delta y} d y & =\int _0^{1} \alpha d x(130 x+10-10) \\ \Delta y & =\left[\frac{\alpha x^{2}}{2} \times 130\right] _0^{1} \\ \Delta y & =1.2 \times 10^{-5} \times 65 \\ \Delta y & =78.0 \times 10^{-5} m=0.78 mm \end{aligned} $$
