Gravitation 5 Question 8
9. Distance between the centres of two stars is $10 a$. The masses of these stars are $M$ and $16 M$ and their radii $a$ and $2 a$ respectively. A body of mass $m$ is fired straight from the surface of the larger star towards the surface of the smaller star. What should be its minimum initial speed to reach the surface of the smaller star? Obtain the expression in terms of $G, M$ and $a$.
(1996, 5M)
Show Answer
Answer:
Correct Answer: 9. $\frac{3 \sqrt{5}}{2} \sqrt{\frac{G M}{a}}$
Solution:
- Let there are two stars 1 and 2 as shown below.
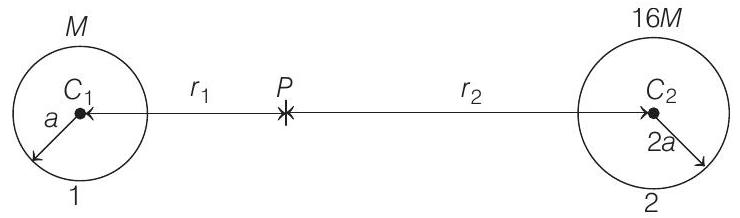
Let $P$ is a point between $C _1$ and $C _2$, where gravitational field strength is zero or at $P$ field strength due to star 1 is equal and opposite to the field strength due to star 2 . Hence,
$$ \begin{aligned} & \frac{G M}{r _1^{2}}=\frac{G(16 M)}{r _2^{2}} \text { or } \frac{r _2}{r _1}=4 \text { also } r _1+r _2=10 a \\ & \therefore \quad r _2=\frac{4}{4+1}(10 a)=8 a \text { and } r _1=2 a \end{aligned} $$
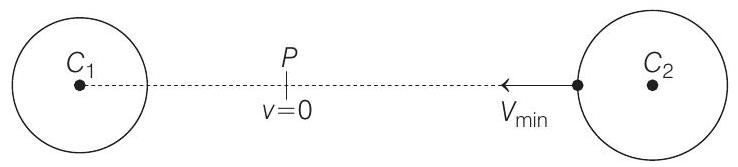
Now, the body of mass $m$ is projected from the surface of larger star towards the smaller one. Between $C _2$ and $P$ it is attracted towards 2 and between $C _1$ and $P$ it will be attracted towards 1. Therefore, the body should be projected to just cross point $P$ because beyond that the particle is attracted towards the smaller star itself.
From conservation of mechanical energy $\frac{1}{2} m v^{2}$ min
= Potential energy of the body at $P$ - Potential energy at the surface of larger star.
$$ \begin{aligned} & \therefore \quad \frac{1}{2} m v _{\min }^{2}=-\frac{G M m}{r _1}-\frac{16 G M m}{r _2} \\ & –\frac{G M m}{10 a-2 a}-\frac{16 G M m}{2 a} \end{aligned} $$
$=-\frac{G M m}{2 a}-\frac{16 G M m}{8 a}–\frac{G M m}{8 a}-\frac{8 G M m}{a}$
or $\quad \frac{1}{2} m v _{\min }^{2}=\frac{45}{8} \frac{G M m}{a}$
$\therefore \quad v _{\min }=\frac{3 \sqrt{5}}{2} \sqrt{\frac{G M}{a}}$






