Gravitation 5 Question 6
7. A spherical body of radius $R$ consists of a fluid of constant density and is in equilibrium under its own gravity. If $P(r)$ is the pressure at $r(r<R)$, then the correct options is/are
(2015 Adv.)
(a) $P(r=0)=0$
(c) $\frac{P \quad r=\frac{3 R}{5}}{P \quad r=\frac{2 R}{5}}=\frac{16}{21}$
(d) $\frac{P \quad r=\frac{R}{2}}{P \quad r=\frac{R}{3}}=\frac{20}{27}$
(b) $\frac{P \quad r=\frac{3 R}{4}}{P \quad r=\frac{2 R}{3}}=\frac{63}{80}$
Show Answer
Answer:
Correct Answer: 7. (b, c)
Solution:
- Gravitational field at a distance $r$ due to mass ’ $m$ '
$E=\frac{G \rho \frac{4}{3} \pi r^{3}}{r^{2}}=\frac{4 G \rho \pi r}{3}$
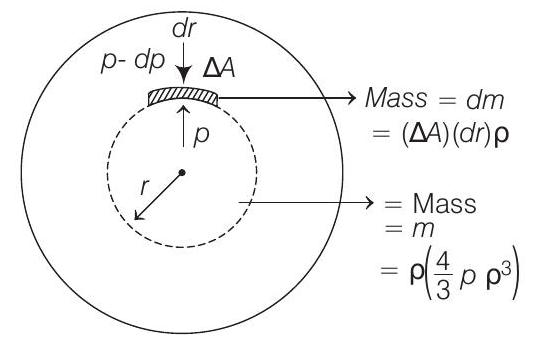
Consider a small element of width $d r$ and area $\Delta A$ at a distance $r$.
Pressure force on this element outwards =gravitational force on ’ $d m$ ’ from ’ $m$ ’ inwards
$$ \begin{array}{ll} \Rightarrow & (d p) \Delta A=E(d m) \\ \Rightarrow & -d p \cdot \Delta A=\frac{4}{3} G \pi \rho r(\Delta A d r \cdot \rho) \end{array} $$
$$ \begin{aligned} & -\int _O^{P} d p=\int _R^{r} \frac{4 G \rho^{2} \pi}{3} r d r \\ & -p=\frac{4 G \rho^{2} \pi}{3 \times 2}\left[r^{2}-R^{2}\right] \Rightarrow p=c\left(R^{2}-r^{2}\right) \\ & \quad r=\frac{3 R}{4}, p _1=c R^{2}-\frac{9 R^{2}}{16}=c \frac{7 R^{2}}{16} \end{aligned} $$
$$ \begin{aligned} & r=\frac{2 R}{3}, p _2=c R^{2}-\frac{4 R^{2}}{9}=c \frac{5 R^{2}}{9} \\ & \frac{p _1}{p _2}=\frac{63}{80} \\ & r=\frac{3 R}{5}, p _3=c R^{2}-\frac{9}{25} R^{2}=c \frac{16 R^{2}}{25} \\ & r=\frac{2 R}{5}, p _4=c R^{2}-\frac{4 R^{2}}{25}=c \frac{21 R^{2}}{25} \\ & \frac{p _3}{p _4}=\frac{16}{21} \end{aligned} $$






