Gravitation 5 Question 5
5. A simple pendulum has a time period $T _1$ when on the earth’s surface and $T _2$ when taken to a height $R$ above the earth’s surface, where $R$ is the radius of the earth. The value of $T _2 / T _1$ is
(a) 1
(b) $\sqrt{2}$
(c) 4
(d) 2
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
- $T \propto \frac{1}{\sqrt{g}}$, i.e. $\frac{T _2}{T _1}=\sqrt{\frac{g _1}{g _2}}$ where, $g _1=$ acceleration due to gravity on earth’s surface $=g$
$g _2=$ acceleration due to gravity at a height $h=R$ from earth’s surface $=g / 4$
$$ \begin{aligned} & \text { Using } g(h)=\frac{g}{1+\frac{h}{R}{ }^{2}} \\ & \Rightarrow \quad \frac{T _2}{T _1}=\sqrt{\frac{g}{g / 4}}=2 \\ & =-V _P \end{aligned} $$
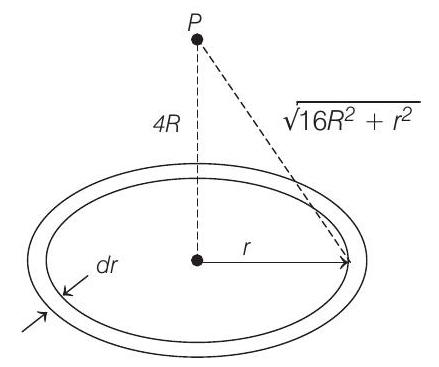
Potential at point $P$ will be obtained by integration as given below.
Let $d M$ be the mass of small ring as shown
$$ \begin{aligned} d M & =\frac{M}{\pi(4 R)^{2}-\pi(3 R)^{2}}(2 \pi r) d r=\frac{2 M r d r}{7 R^{2}} \\ d V _P & =-\frac{G d M}{\sqrt{16 R^{2}+r^{2}}} \\ & =-\frac{2 G M}{7 R^{2}} \int _{3 R}^{4 R} \frac{r}{\sqrt{16 R^{2}+r^{2}}} d r \\ & =-\frac{2 G M}{7 R}(4 \sqrt{2}-5) \\ \therefore \quad W & =+\frac{2 G M}{7 R}(4 \sqrt{2}-5) \end{aligned} $$






