Gravitation 5 Question 4
4. Four particles, each of mass $M$ and equidistant from each other, move along a circle of radius $R$ under the action of their mutual gravitational attraction, the speed of each particle is
(a) $\sqrt{\frac{G M}{R}}$
(b) $\sqrt{2 \sqrt{2} \frac{G M}{R}}$
(c) $\sqrt{\frac{G M}{R}(1+2 \sqrt{2})}$
(d) $\frac{1}{2} \sqrt{\frac{G M}{R}(1+2 \sqrt{2})}$
(2014 Main)
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Net force acting on any one particle $M$,
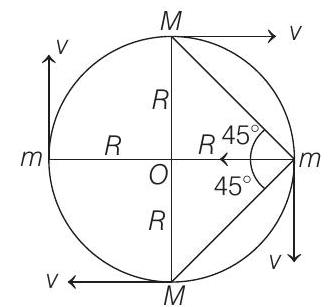
$$ \begin{aligned} & =\frac{G M^{2}}{(2 R)^{2}}+\frac{G M^{2}}{(R \sqrt{2})^{2}} \cos 45^{\circ}+\frac{G M^{2}}{(R \sqrt{2})^{2}} \cos 45^{\circ} \\ & =\frac{G M^{2}}{R^{2}} \frac{1}{4}+\frac{1}{\sqrt{2}} \end{aligned} $$
This force will equal to centripetal force.
So, $\frac{M v^{2}}{R}=\frac{G M^{2}}{R^{2}} \frac{1}{4}+\frac{1}{\sqrt{2}}$
$$ v=\sqrt{\frac{G M}{4 R}(1+2 \sqrt{2})}=\frac{1}{2} \sqrt{\frac{G M}{R}(2 \sqrt{2}+1)} $$
Hence, speed of each particle in a circular motion is
$$ \frac{1}{2} \sqrt{\frac{G M}{R}(2 \sqrt{2}+1)} $$






