SATHEE: Gravitation 5 Question 1

Gravitation 5 Question 1

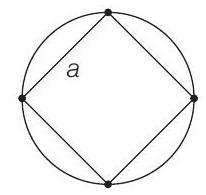1. Four identical particles of mass $M$ are located at the corners of a square of side $a$ . What should be their speed, if each of them revolves under the influence of other’s gravitational field in a circular orbit

circumscribing the square?

(a) $1.35 \sqrt{\frac{G M}{a}}$

(b) $1.16 \sqrt{\frac{G M}{a}}$

(d) $1.41 \sqrt{\frac{G M}{a}}$

(Main 2019, 8 April I)

Show Answer

Answer:

Correct Answer: 1. (b)

Solution:

In given configuration of masses, net gravitational force provides the necessary centripetal force for rotation.

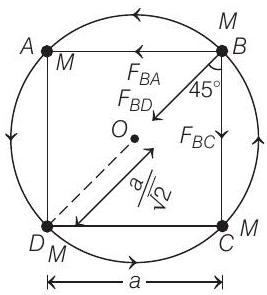
Net force on mass $M$ at position $B$ towards centre of circle is $F_{B O net} = F_{B D} + F_{B A} \sin 45^{\circ} + F_{B C} \cos 45^{\circ}$

$= \frac{G M^{2}}{(\sqrt{2} a)^{2}} + \frac{G M^{2}}{a^{2}} \frac{1}{\sqrt{2}} + \frac{G M^{2}}{a^{2}} \frac{1}{\sqrt{2}}$

[where, diagonal length $B D$ is $\sqrt{2} a$ ]

$= \frac{G M^{2}}{2 a^{2}} + \frac{G M^{2}}{a^{2}} \frac{2}{\sqrt{2}} = \frac{G M^{2}}{a^{2}} \frac{1}{2} + \sqrt{2}$

This force will act as centripetal force.

Distance of particle from centre of circle is $\frac{a}{\sqrt{2}}$ .

Here, $F_{centripetal} = \frac{M v^{2}}{r} = \frac{M v^{2}}{\frac{a}{\sqrt{2}}} = \frac{\sqrt{2} M v^{2}}{a} ∵ r = \frac{a}{\sqrt{2}}$

So, for rotation about the centre,

$F_{centripetal} = F_{B O (net)}$

$\Rightarrow \sqrt{2} \frac{M v^{2}}{a} = \frac{G M^{2}}{a^{2}} \frac{1}{2} + \sqrt{2}$

$\Rightarrow v^{2} = \frac{G M}{a} 1 + \frac{1}{2 \sqrt{2}} = \frac{G M}{a} (1.35) \Rightarrow v = 1.16 \sqrt{\frac{G M}{a}}$

पिछला

अगला

Gravitation 5 Question 1

1. Four identical particles of mass $M$ are located at the corners of a square of side $a$ . What should be their speed, if each of them revolves under the influence of other’s gravitational field in a circular orbit

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Gravitation 5 Question 1

1. Four identical particles of mass M are located at the corners of a square of side a. What should be their speed, if each of them revolves under the influence of other’s gravitational field in a circular orbit

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

1. Four identical particles of mass $M$ are located at the corners of a square of side $a$ . What should be their speed, if each of them revolves under the influence of other’s gravitational field in a circular orbit