Gravitation 3 Question 10
13. Two satellites $S _1$ and $S _2$ revolve round a planet in coplanar circular orbits in the same sense. Their periods of revolution are $1 h$ and $8 h$, respectively. The radius of the orbit of $S _1$ is $10^{4} km$ when $S _2$ is closest to $S _1$. Find
$(1986,6 M)$
(a) the speed of $S _2$ relative to $S _1$,
(b) the angular speed of $S _2$ as actually observed by an astronaut in $S _1$.
Show Answer
Solution:
- $T \propto r^{3 / 2}$ or $r \propto T^{2 / 3} \Rightarrow \frac{r _2}{r _1}={\frac{T _2}{T _1}}^{2 / 3}$
$$ \begin{aligned} r _2 & ={\frac{T _2}{T _1}}^{2 / 3} \quad r _1=\frac{8}{1}^{2 / 3}\left(10^{4}\right) \\ & =4 \times 10^{4} km \end{aligned} $$
Now, $\quad v _1=\frac{2 \pi r _1}{T _1}=\frac{(2 \pi)\left(10^{4}\right)}{1}=2 \pi \times 10^{4} km / h$
$v _2=\frac{2 \pi r _2}{T _2}=\frac{(2 \pi)\left(4 \times 10^{4}\right)}{8}=\left(\pi \times 10^{4}\right) km / h$
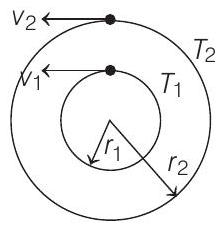
(a) Speed of $S _2$ relative to $S _1=v _2-v _1=-\pi \times 10^{4} km / h$
(b) Angular speed of $S _2$ as observed by $S _1$
$$ \begin{aligned} \omega _r & =\frac{\left|v _2-v _1\right|}{\left|r _2-r _1\right|}=\frac{\pi \times 10^{4} \times \frac{5}{18} m / s}{\left(3 \times 10^{7} m\right)} \\ & =0.3 \times 10^{-3} rad / s \\ & =3.0 \times 10^{-4} rad / s \end{aligned} $$






