Gravitation 2 Question 3
6. From a solid sphere of mass $M$ and radius $R$, a spherical portion of radius $\frac{R}{2}$ is removed as shown in the figure. Taking gravitational potential $V=0$ at $r=\infty$, the potential at the centre of the cavity thus formed is ( $G$ = gravitational constant)
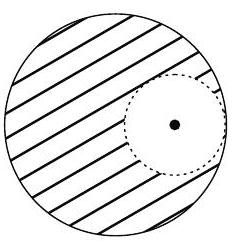
(2015 Main)
(a) $\frac{-G M}{R}$
(b) $\frac{-G M}{2 R}$
(c) $\frac{-2 G M}{3 R}$
(d) $\frac{-2 G M}{R}$
Show Answer
Answer:
Correct Answer: 6. (a)
Solution:
- $V _R=V _T-V _C$
$V _R=$ Potential due to remaining portion
$V _T=$ Potential due to total sphere
$V _C=$ Potential due to cavity
Radius of cavity is $\frac{R}{2}$. Hence, volume and mass is $\frac{M}{8}$.
$\therefore V _R=-\frac{G M}{R^{3}} 1.5 R^{2}-0.5 \frac{R^{2}}{2}+\frac{G \frac{M}{8}}{\frac{R}{2}} \frac{3}{2}=-\frac{G M}{R}$
