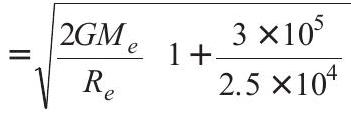Gravitation 2 Question 1
4. A rocket is launched normal to the surface of the Earth, away from the Sun, along the line joining the Sun and the Earth. The Sun is
(a)
(b)
(c)
(d)
(2017 Adv.)
Show Answer
Answer:
Correct Answer: 4. (c)
Solution:
- Given,
From energy conservation,
Here,
Given,