Electrostatics 7 Question 3
3. There is uniform spherically symmetric surface charge density at a distance
(Main 2019, 12 Jan I) (a)
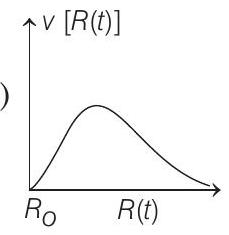
(c)
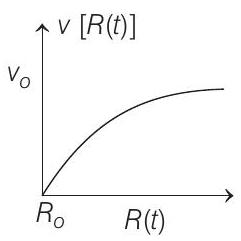
(b)
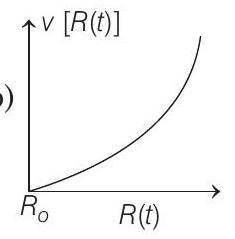
(d)
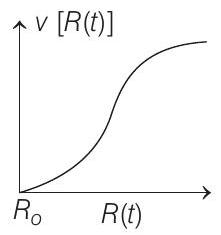
Show Answer
Solution:
- Key Idea As, electrostatic force is conserved in nature so, total energy of charge distribution remains constant in absence of any external interaction.
Let radius of distribution at some instant
Now by conservation of energy, we have
(
Differentiating this equation with respect to
Here,
Also, slope
From above conclusions, we can see that the best suited graph is given in option (c).






