Electrostatics 7 Question 28
30. A small ball of mass $2 \times 10^{-3} kg$ having a charge of $1 \mu C$ is suspended by a string of length $0.8 m$. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity which should be imparted to the lower ball, so that it can make complete revolution.
$(2001,5 M)$
Show Answer
Solution:
- Given : $q=1 \mu C=10^{-6} C$
$$ \begin{aligned} m & =2 \times 10^{-3} kg \\ \text { and } \quad l & =0.8 m \end{aligned} $$
Let $u$ be the speed of the particle at its lowest point and $v$ its speed at highest point.
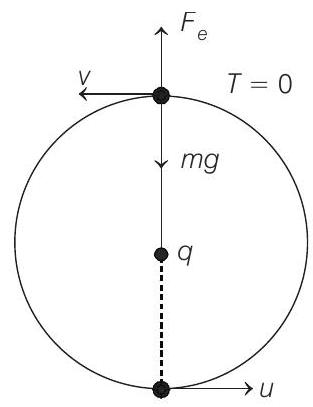
At highest point three forces are acting on the particle.
(a) Electrostatic repulsion
$$ F _e=\frac{1}{4 \pi \varepsilon _0} \frac{q^{2}}{l^{2}} $$
(outwards)
(b) Weight $w=m g$
(inwards)
(c) Tension $T$
(inwards)
$T=0$, if the particle has just to complete the circle and the necessary centripetal force is provided by $w-F _e$ i.e.
or
$$ \frac{m v^{2}}{l}=w-F _e $$
$$ v^{2}=\frac{0.8}{2 \times 10^{3}} \quad 2 \times 10^{-3} \times 10-\frac{9.0 \times 10^{9} \times\left(10^{-6}\right)^{2}}{(0.8)^{2}} m^{2} / s^{2} $$
or $\quad v^{2}=2.4 m^{2} / s^{2}$
Now, the electrostatic potential energy at the lowest and highest points are equal. Hence, from conservation of mechanical energy.
Increase in gravitational potential energy
$=$ Decrease in kinetic energy.
or
$$ \begin{aligned} m g(2 l) & =\frac{1}{2} m\left(u^{2}-v^{2}\right) \\ u^{2} & =v^{2}+4 g l \end{aligned} $$
Substituting the values of $v^{2}$ from Eq. (i), we get
$$ \begin{array}{rlrl} & & u^{2} & =2.4+4(10)(0.8)=34.4 m^{2} / s^{2} \\ \therefore & u & =5.86 m / s \end{array} $$
Therefore, minimum horizontal velocity imparted to the lower ball, so that it can make complete revolution, is $5.86 m / s$.






