Electrostatics 7 Question 18
20. A uniform magnetic field
(2017 Main) Which of the following option(s) is/are correct?
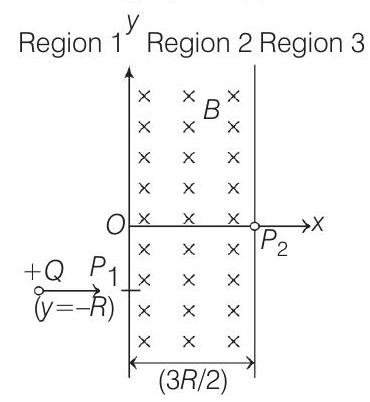
(a) When the particle re-enters region 1 through the longest possible path in region 2 , the magnitude of the change in its linear momentum between point
(b) For
(c) For
(d) For a fixed
Show Answer
Solution:
- (a)
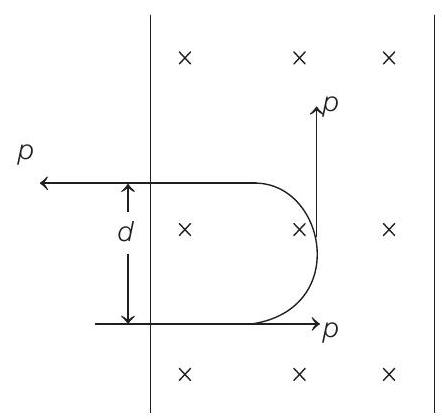
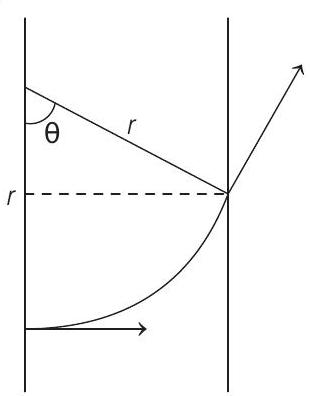
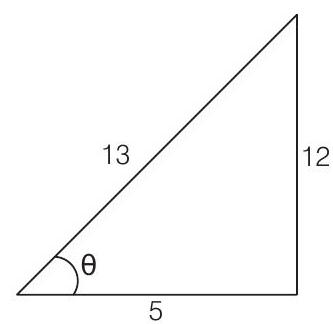
(c)
(d)






