SATHEE: Electrostatics 7 Question 15

Electrostatics 7 Question 15

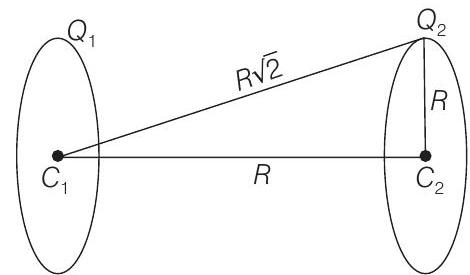
15. Two identical thin rings, each of radius $R$ , are coaxially placed a distance $R$ apart. If $Q_{1}$ and $Q_{2}$ are respectively the charges uniformly spread on the two rings, the work done in moving a charge $q$ from the centre of one ring to that of the other is

(1992, 2M)

(a) zero

(b) $\frac{q (Q_{1} - Q_{2}) (\sqrt{2} - 1)}{\sqrt{2} (4 π ε_{0} R)}$

(d) $q (Q_{1} / Q_{2}) (\sqrt{2} + 1) \sqrt{2} (4 π ε_{0} R)$

Passage Based Questions

Passage

Consider an evacuated cylindrical chamber of height $h$ having rigid conducting plates at the ends and an insulating curved surface as shown in the figure. A number of spherical balls made of a light weight and soft material and coated with a conducting material are placed on the bottom plate. The balls have a radius $r « h$ . Now, a high voltage source (HV) connected across the conducting plates such that the bottom plate is at $+ V_{0}$ and the top plate at $- V_{0}$ . Due to their conducting surface, the balls will get charge, will become equipotential with the plate and are repelled by it. The balls will eventually collide with the top plate, where the coefficient of restitution can be taken to be zero due to te soft nature of the material of the balls. The electric field in the chamber can be considered to be that of a parallel plate capacitor. Assume that there are no collisions between the balls and the interaction between them is negligible. (Ignore gravity)

Show Answer

Solution:

$V_{C_{1}} = V_{Q_{1}} + V_{Q_{2}} = \frac{1}{4 π ε_{0}} \frac{Q_{1}}{R} + \frac{1}{4 π ε_{0}} \frac{Q_{2}}{R \sqrt{2}}$

$= \frac{1}{4 π ε_{0} R} Q_{1} + \frac{Q_{2}}{\sqrt{2}}$

Similarly $V_{C_{2}} = \frac{1}{4 π ε_{0} R} Q_{2} + \frac{Q_{1}}{\sqrt{2}}$

$∴ Δ V = V_{C_{1}} - V_{C_{2}} = \frac{1}{4 π ε_{0} R} (Q_{1} - Q_{2}) - \frac{1}{\sqrt{2}} (Q_{1} - Q_{2})$

$\begin{aligned} = \frac{Q_{1} - Q_{2}}{\sqrt{2} (4 π ε_{0} R)} (\sqrt{2} - 1) \\ W & = q Δ V = q (Q_{1} - Q_{2}) (\sqrt{2} - 1) / \sqrt{2} (4 π ε_{0} R) \end{aligned}$