Electrostatics 6 Question 8
8. At $t=0$, switch $S$ is closed. The charge on the capacitor is varying with time as $Q=Q _0\left(1-e^{-\alpha t}\right)$. Obtain the value of $Q _0$ and $\alpha$ in the given circuit parameters.
$(2005,4$ M)
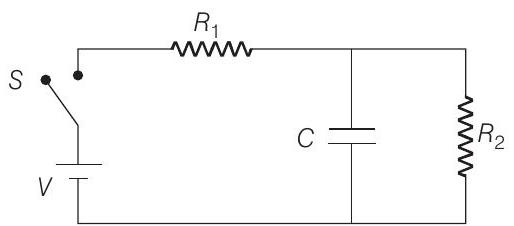
Show Answer
Solution:
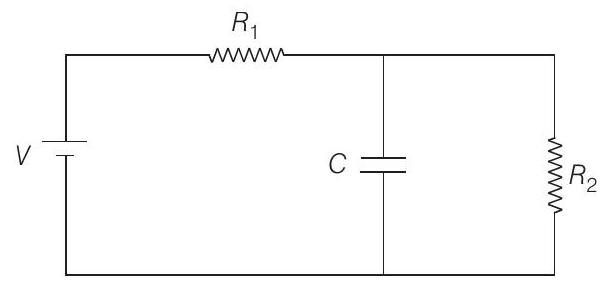
$Q _0$ is the steady state charge stored in the capacitor.
$Q _0=C[PD$ across capacitor in steady state $]$
$=C$ [steady state current through $\left.R _2\right]\left(R _2\right)$
$$ \begin{aligned} & \quad=C \frac{V}{R _1+R _2} \cdot R _2 \\ & \therefore \quad Q _0=\frac{C V R _2}{R _1+R _2} \\ & \alpha \text { is } 1 / \tau _c \text { or } \frac{1}{C R _{\text {net }}} \end{aligned} $$
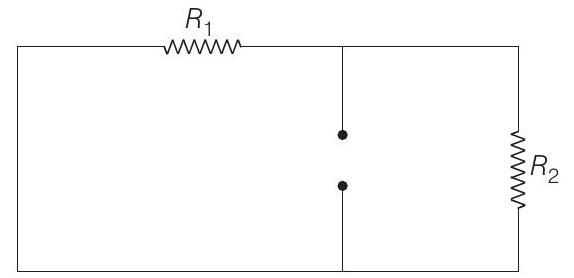
Here, $R _{\text {net }}$ is equivalent resistance across capacitor after short circuiting the battery. Thus,
$$ \begin{aligned} R _{\text {net }} & =\frac{R _1 R _2}{R _1+R _2} \quad\left(\text { As } R _1 \text { and } R _2 \text { are in parallel }\right) \\ \alpha & =\frac{1}{C \frac{R _1 R _2}{R _1+R _2}}=\frac{R _1+R _2}{C R _1 R _2} \end{aligned} $$






