Electrostatics 6 Question 3
3. A $4 \mu F$ capacitor and a resistance of $2.5 M \Omega$ are in series with $12 V$ battery. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [Given, $\ln (2)=0.693$ ]
(2005, 2M)
(a) $13.86 s$
(b) $6.93 s$
(c) $7 s$
(d) $14 s$
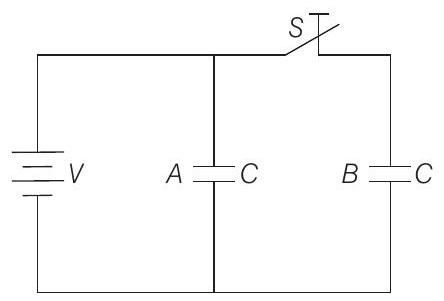
relative permittivity) 3 . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
$(1983,6 M)$
Show Answer
Solution:
- Given : $V _C=3 V _R=3\left(V-V _C\right)$
Here, $V$ is the applied potential.
$$ \begin{array}{ll} \therefore & V _C=\frac{3}{4} V \quad \text { or } \quad V\left(1-e^{-t / \tau _c}\right)=\frac{3}{4} V \\ \therefore & e^{-t / \tau _c}=\frac{1}{4} \end{array} $$
Here,
$$ \tau _c=C R=10 s $$
Substituting this value of $\tau _c$ in Eq. (i) and solving for $t$, we get
$$ t=13.86 s $$
$\therefore$ Correct answer is (a).






