Electrostatics 6 Question 11
11. In the given circuit,
$(1988,5 M)$
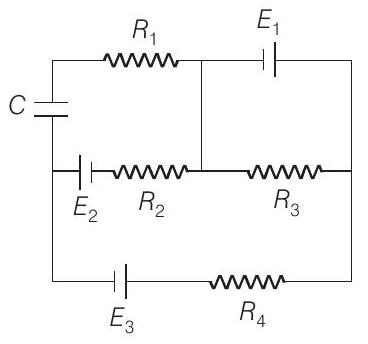
$E _1=3 E _2=2 E _3=6 V$ and $R _1=2 R _4=6 \Omega$,
$R _3=2 R _2=4 \Omega, C=5 \mu F$.
Find the current in $R _3$ and the energy stored in the capacitor.
Show Answer
Solution:
- In steady state no current will flow through $R _1=6 \Omega$.
Potential difference across $R _3$ or $4 \Omega$ is $E _1$ or $6 V$
$\therefore$ Current through it will be $\frac{6}{4}=1.5 A$ from right to left.
Because left hand side of this resistance is at higher potential.
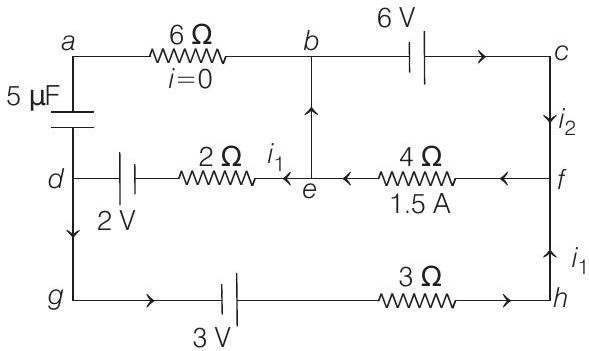
Now, suppose this $1.5 A$ distributes in $i _1$ and $i _2$ as shown.
Applying Kirchhoff’s second law in loop dghfed
$$ \begin{array}{cc} 3-3 i _1-4 \times 1.5-2 i _1+2=0 \\ \therefore & i _1=-\frac{1}{5} A=-0.2 A \end{array} $$
To find energy stored in capacitor we will have to find potential difference across it. Or $V _{a d}$.
Now,
$$ V _a-2 i _1+2=V _d $$
$$ \begin{array}{ll} \text { or } & V _a-V _d=2 i _1-2=-2.4 V \\ \text { or } & V _d-V _a=2.4 V=V _{d a} \end{array} $$
Energy stored in capacitor:
$$ \begin{aligned} U & =\frac{1}{2} C V _{d a}^{2} \\ & =\frac{1}{2}\left(5 \times 10^{-6}\right)(2.4)^{2} \\ & =1.44 \times 10^{-5} J \end{aligned} $$






