Electrostatics 6 Question 10
10. A leaky parallel plate capacitor is filled completely with a material having dielectric constant $K=5$ and electrical conductivity $\sigma=7.4 \times 10^{-12} \Omega^{-1} m^{-1}$. If the charge on the capacitor at instant $t=0$ is $q=8.85 \mu C$, then calculate the leakage current at the instant $t=12 s$.
(1997 C, 5M)
Show Answer
Solution:
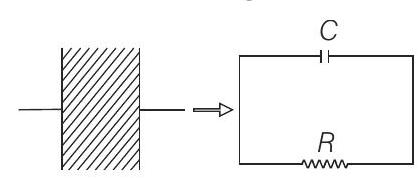
- The problem is basically of discharging of $C R$ circuit, because between the plates of the capacitor, there is capacitor as well as resistance.
$$ \begin{array}{rlrl} R & =\frac{d}{\sigma A} \quad R=\frac{l}{\sigma A} \\ \text { and } & C & =\frac{K \varepsilon _0 A}{d} & \end{array} $$
$\therefore$ Time constant, $\tau _c=C R=\frac{K \varepsilon _0}{\sigma}$
Substituting the values, we have
$$ \tau _c=\frac{5 \times 8.86 \times 10^{-12}}{7.4 \times 10^{-12}}=5.98 s $$
Charge at any time decreases exponentially as
$$ q=q _0 e^{-t / \tau _c} $$
Here, $q _0=8.85 \times 10^{-6} C($ Charge at time $t=0)$
Therefore, discharging (leakage) current at time $t$ will be given by
$$ i=-\frac{d q}{d t}=\frac{q _0}{\tau _c} e^{-t / \tau _c} $$
or current at $t=12 s$ is
$$ \begin{aligned} i & =\frac{\left(8.85 \times 10^{-6}\right)}{5.98} e^{-12 / 5.98} \\ & =0.198 \times 10^{-6} A=0.198 \mu A \\ i & =0.198 \mu A \end{aligned} $$






