Electrostatics 5 Question 4
4. Figure shows charge $(q)$ versus voltage $(V)$ graph for series and parallel combination of two given capacitors. The capacitances are
(Main 2019, 10 April I)
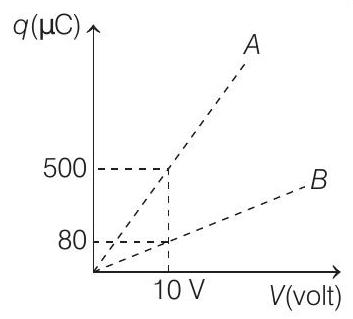
(a) $60 \mu F$ and $40 \mu F$
(b) $50 \mu F$ and $30 \mu F$
(c) $20 \mu F$ and $30 \mu F$
(d) $40 \mu F$ and $10 \mu F$
5 The parallel combination of two air filled parallel plate capacitors of capacitance $C$ and $n C$ is connected to a battery of voltage, $V$. When the capacitors are fully charged, the battery is removed and after that a dielectric material of dielectric constant $K$ is placed between the two plates of the first capacitor. The new potential difference of the combined system is
(a) $\frac{(n+1) V}{(K+n)}$
(b) $\frac{n V}{K+n}$
(c) $V$
(d) $\frac{V}{K+n}$
(Main 2019, 9 April II)
Show Answer
Answer:
Correct Answer: 4. (b)
Solution:
- In the given figure,
Slope of $O A>$ Slope of $O B$
Since, we know that, net capacitance of parallel combination $>$ net capacitance of series combination
$\therefore$ Parallel combination’s capacitance,
$$ C _P=C _1+C _2=\frac{500 \mu C}{10 V}=50 \mu F $$
Series combination’s capacitance,
$$ C _S=\frac{C _1 C _2}{C _1+C _2}=\frac{80 \mu C}{10 V}=8 \mu F $$
or
$$ \begin{aligned} C _1 C _2 & =8 \times\left(C _1+C _2\right)=8 \times 50 \mu F \\ & =400 \mu F \quad \text { [using Eq. (i)] } \end{aligned} $$
From Eqs. (i) and (iii), we get
$$ \begin{aligned} & C _1=50-C _2 \\ & \text { and } \quad C _1 C _2=400 \\ & \Rightarrow \quad C _2\left(50-C _2\right)=400 \\ & \Rightarrow \quad 50 C _2-C _2^{2}=400 \\ & \text { or } C _2^{2}-50 C _2+400=0 \\ & \Rightarrow C _2=\frac{+50 \pm \sqrt{2500-1600}}{2}=\frac{+50 \pm 30}{2} \end{aligned} $$
$\Rightarrow \quad C _2=+40 \mu F$ or $+10 \mu F$
Also, $C _1=50-C _2 \Rightarrow C _1=+10 \mu F$ or $+40 \mu F$
Hence, capacitance of two given capacitors is $10 \mu F$ and $40 \mu F$.
