Electrostatics 5 Question 28
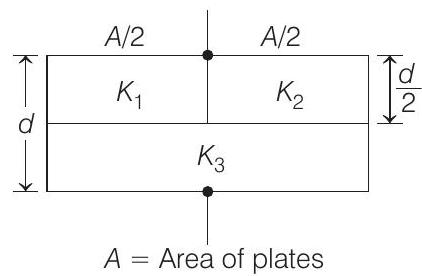
30. A parallel plate capacitor of area $A$, plate separation $d$ and capacitance $C$ is filled with three different dielectric materials having dielectric constants $K _1, K _2$ and $K _3$ as shown. If a single dielectric material is to be used to have the same capacitance $C$ in this capacitor then its dielectric constant $K$ is given by
$(2000,2 M)$
(a) $\frac{1}{K}=\frac{1}{K _1}+\frac{1}{K _2}+\frac{1}{2 K _3}$
(b) $\frac{1}{K}=\frac{1}{K _1+K _2}+\frac{1}{2 K _3}$
(c) $\frac{1}{K}=\frac{K _1 K _2}{K _1+K _2}+2 K _3$
(d) $K=\frac{K _1 K _3}{K _1+K _3}+\frac{K _2 K _3}{K _2+K _3}$
Show Answer
Solution:
- Applying $C=\frac{\varepsilon _0 A}{d-t _1-t _2+\frac{t _1}{K _1}+\frac{t _2}{K _2}}$, we have
$\frac{\varepsilon _0(A / 2)}{d-d / 2-d / 2+\frac{d / 2}{K _1}+\frac{d / 2}{K _3}}$
$$ +\frac{\varepsilon _0(A / 2)}{d-d / 2-d / 2+\frac{d / 2}{K _2}+\frac{d / 2}{K _3}}=\frac{K \varepsilon _0 A}{d} $$
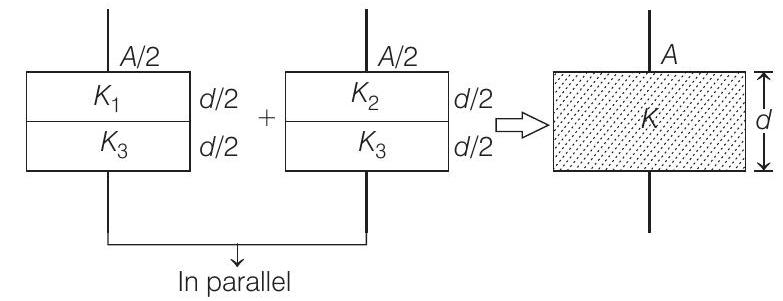
Solving this equation, we get
$$ K=\frac{K _1 K _3}{K _1+K _3}+\frac{K _2 K _3}{K _2+K _3} $$
