Electrostatics 5 Question 14
15. An electric line of force in the $x-y$ plane is given by the equation $x^{2}+y^{2}=1$. A particle with unit positive charge, initially at rest at the point $x=1, y=0$ in the $x-y$ plane, will move along the circular line of force.
$(1988,2 M)$
Analytical & Descriptive Questions
Show Answer
Solution:
- In the given arrangement, capacitor can be viewed as threedifferent capacitors connected in parallel as shown below,
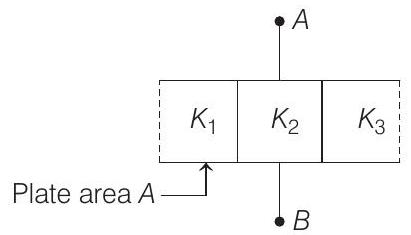
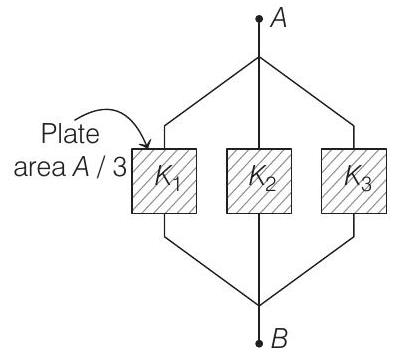
So, equivalent capacity of the system is
$$ \begin{aligned} C _{eq} & =C _1+C _2+C _3 \\ \Rightarrow \frac{K \varepsilon _0 A}{d} & =\frac{K _1 \varepsilon _0 A / 3}{d}+\frac{K _2 \varepsilon _0 A / 3}{d}+\frac{K _3 \varepsilon _0 A / 3}{d} \\ \Rightarrow \quad K & =\frac{K _1}{3}+\frac{K _2}{3}+\frac{K _3}{3} \\ \text { Here, } K _1 & =10, K _2=12 \text { and } K _3=14 \\ \text { So, } \quad K & =\frac{10+12+14}{3} \Rightarrow K=12 \end{aligned} $$
16 This capacitor system can be converted into two parts as shown in the figure
$d / 2 \quad d / 2$
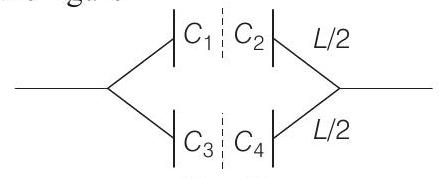
where $C _1, C _2, C _3$ and $C _4$ are capacitance of the capacitor having dielectric constants $K _1, K _2, K _3$ and $K _4$ respectively.
Here, $\quad C _1=\frac{K _1 \varepsilon _0 A / 2}{d / 2}=\frac{K _1 \varepsilon _0 A}{d}$
Similarly, $C _2=\frac{K _2 \varepsilon _0 A}{d}, C _3=\frac{K _3 \varepsilon _0 A}{d}$ and $C _4=\frac{K _4 \varepsilon _0 A}{d}$
Since, equivalent capacitance in series combination is
$$ C _{eq}=\frac{C _1 \cdot C _2}{C _1+C _2} $$
Here, $C _1, C _2$ and $C _3, C _4$ are in series combination.
$$ \begin{aligned} \therefore\left(C _{\text {eq }}\right) _{12} & =\frac{C _1 \cdot C _2}{C _1+C _2}=\frac{\frac{K _1 \varepsilon _0 A}{d} \cdot \frac{K _2 \varepsilon _0 A}{d}}{\frac{K _1 \varepsilon _0 A}{d}+\frac{K _2 \varepsilon _0 A}{d}} \\ & =\frac{K _1 \cdot K _2}{K _1+K _2} \cdot \frac{\varepsilon _0 A}{d} \end{aligned} $$
Similarly, $\left(C _{eq}\right) _{34}=\frac{K _3 \cdot K _4}{K _3+K _4} \cdot \frac{\varepsilon _0 A}{d}$
Now, $\left(C _{\text {eq }}\right) _{12}$ and $\left(C _{\text {eq }}\right) _{34}$ are in parallel combination.
$\therefore \quad C _{\text {net }}=\left(C _{\text {eq }}\right) _{12}+\left(C _{\text {eq }}\right) _{34}$
$$ =\frac{K _1 \cdot K _2}{K _1+K _2} \cdot \frac{\varepsilon _0 A}{d}+\frac{K _3 \cdot K _4}{K _3+K _4} \cdot \frac{\varepsilon _0 A}{d} $$
$\Rightarrow \quad C _{\text {net }}=\frac{K _1 \cdot K _2}{K _1+K _2}+\frac{K _3 \cdot K _4}{K _3+K _4} \frac{\varepsilon _0 A}{d}$
If $K$ is effective dielectric constant, then
$$ C _{\text {net }}=\frac{K \varepsilon _0 A}{d} $$
From Eqs. (i) and (ii),
$$ \begin{aligned} \frac{K \varepsilon _0 A}{d} & =\frac{K _1 \cdot K _2}{K _1+K _2}+\frac{K _3 \cdot K _4}{K _3+K _4} \frac{\varepsilon _0 A}{d} \\ K & =\frac{K _1 \cdot K _2}{K _1+K _2}+\frac{K _3 \cdot K _4}{K _3+K _4} \end{aligned} $$
or
