Electrostatics 3 Question 6
6. Consider a uniform spherical charge distribution of radius $R _1$ centred at the origin $O$. In this distribution, a spherical cavity of radius $R _2$, centred at $P$ with distance $O P=a=R _1-R _2$ (see figure) is made. If the electric field inside the cavity at position $\mathbf{r}$ is $\mathbf{E}(\mathbf{r})$, then the correct statements is/are
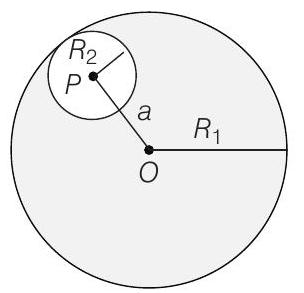
(a) $\mathbf{E}$ is uniform, its magnitude is independent of $R _2$ but its direction depends on $\mathbf{r}$
(b) $\mathbf{E}$ is uniform, its magnitude depends on $R _2$ and its direction depends on $\mathbf{r}$
(c) $\mathbf{E}$ is uniform, its magnitude is independent of ’ $a$ ’ but its direction depends on a
(d) $\mathbf{E}$ is uniform and both its magnitude and direction depend on a
Show Answer
Answer:
Correct Answer: 6. (a)
Solution:
- The sphere with cavity can be assumed as a complete sphere with positive charge of radius $R _1$ + another complete sphere with negative charge and radius $R _2$.
$E _{+} \rightarrow \mathbf{E}$ due to total positive charge
$E _{-} \rightarrow \mathbf{E}$ due to total negative charge.
$$ E=E _{+}+E _{-} $$
If we calculate it at $P$, then $E _{-}$comes out to be zero.
$\therefore \quad E=E _{+}$
and $E _{+}=\frac{1}{4 \pi \varepsilon _0} \frac{q}{R _1^{3}}(O P)$, in the direction of $O P$.
Here, $q$ is total positive charge on whole sphere.
It is in the direction of $O P$ or $\mathbf{a}$.
Now, inside the cavity electric field comes out to be uniform at any point. This is a standard result.






