Electrostatics 3 Question 5
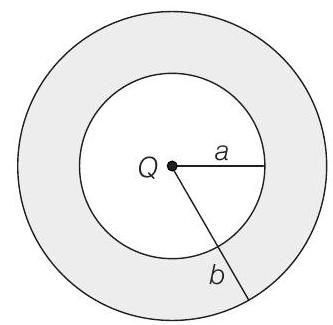
5. The region between two concentric spheres of radii $a$ and $b$, respectively (see the figure), has volume charge density $\rho=\frac{A}{r}$, where, $A$ is a constant and $r$ is the distance from the centre. At the centre of the spheres is a point charge $Q$. The value of $A$, such that the electric field in the region between the spheres will be constant, is
(2016 Main)
(a) $\frac{Q}{2 \pi a^{2}}$
(b) $\frac{Q}{2 \pi\left(b^{2}-a^{2}\right)}$
(c) $\frac{2 Q}{\pi\left(a^{2}-b^{2}\right)}$
(d) $\frac{2 Q}{\pi a^{2}}$
Show Answer
Answer:
Correct Answer: 5. (a)
Solution:
- As $E$ is constant,
Hence, $E _a=E _b$
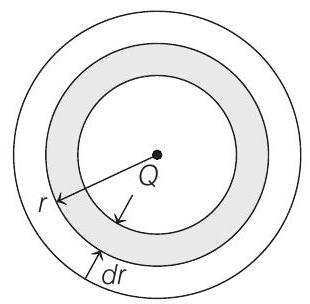
As per Guass theorem, only $Q _{\text {in }}$ contributes in electric field.
$$ \therefore \quad \frac{k Q}{a^{2}}=\frac{k Q+\int _a^{b} 4 \pi r^{2} d r \cdot \frac{A}{r}}{b^{2}} $$
Here, $\quad k=\frac{1}{4 \pi \varepsilon _0}$
$$ \Rightarrow \quad Q \frac{b^{2}}{a^{2}}=Q+\left.4 \pi A \frac{r^{2}}{2}\right| _a ^{b}=Q+4 \pi A \cdot \frac{b^{2}-a^{2}}{2} $$
$$ \Rightarrow \quad Q \frac{b^{2}}{a^{2}}=Q+2 \pi A\left(b^{2}-a^{2}\right) $$
$\Rightarrow \quad Q \frac{b^{2}-a^{2}}{a^{2}}=2 \pi A\left(b^{2}-a^{2}\right) \Rightarrow A=\frac{Q}{2 \pi a^{2}}$






