Electrostatics 2 Question 8
8. A uniformly charged ring of radius $3 a$ and total charge $q$ is placed in $x y$-plane centred at origin. A point charge $q$ is moving towards the ring along the $Z$-axis and has speed $v$ at $z=4 a$. The minimum value of $v$ such that it crosses the origin is
(Main 2019, 10 April I)
(a) $\sqrt{\frac{2}{m}} \frac{1}{5} \frac{q^{2}}{4 \pi \varepsilon _0 a}$
(b) $\sqrt{\frac{2}{m}} \frac{4}{15} \frac{q^{2}}{4 \pi \varepsilon _0 a}$
(c) $\sqrt{\frac{2}{m}} \frac{1}{15} \frac{q^{2}}{4 \pi \varepsilon _0 a}$
(d) $\sqrt{\frac{2}{m}} \frac{2}{15} \frac{q^{2}}{4 \pi \varepsilon _0 a}$ $1 / 2$
Show Answer
Answer:
Correct Answer: 8. (b)
Solution:
- Potential at any point at distance $x$ from the centre of the ring is given by
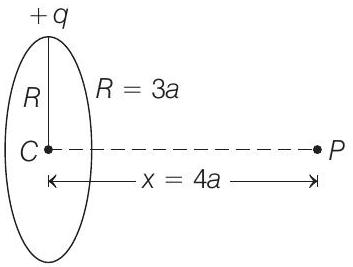
$$ V _p=\frac{K q}{\sqrt{R^{2}+x^{2}}} $$
Given, $\quad R=3 a$ and $x=4 a$
$$ \therefore \quad V _P=\frac{K q}{\sqrt{9 a^{2}+16 a^{2}}}=\frac{K q}{5 a} $$
At centre, $x=0$
So, potential at centre is
$$ V _C=\frac{K q}{R}=\frac{K q}{3 a} $$
Now, energy required to get this charge from $x=4 a$ to the centre is
$$ \begin{aligned} \Delta U=q \Delta V & =q\left[V _C-V _P\right]=q \frac{K q}{3 a}-\frac{K q}{5 a} \\ & =\frac{K q^{2}}{a} \frac{1}{3}-\frac{1}{5} \\ \Delta U & =\frac{2}{15} \frac{K q^{2}}{a} \end{aligned} $$
This energy must be equal to (or less than) the kinetic energy of the charge, i.e.
$$ \frac{1}{2} m v^{2} \geq \frac{2}{15} \frac{K q^{2}}{a} $$
So, minimum energy required is
$$ \frac{1}{2} m v^{2}=\frac{2}{15} \times \frac{1}{4 \pi \varepsilon _0} \times \frac{q^{2}}{a} \quad\left(\text { put } K=1 / 4 \pi \varepsilon _0\right) $$
$\therefore$ Minimum velocity,
or
$$ \begin{aligned} v^{2} & =\frac{2}{m} \times \frac{2}{4 \pi \varepsilon _0} \times \frac{q^{2}}{15 a} \\ v & =\sqrt{\frac{2}{m}} \times \sqrt{\frac{2 q^{2}}{4 \pi \varepsilon _0 a \times 15}} \end{aligned} $$






