Electrostatics 2 Question 6
6. Four equal point charges
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 6. (d)
Solution:
- The four charges are shown in the figure below,
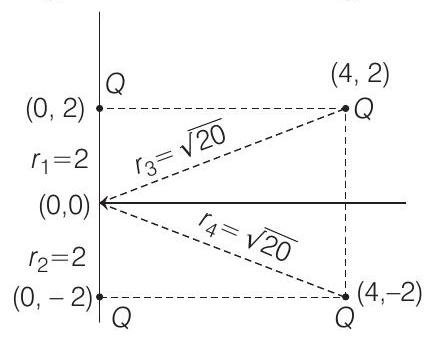
Electric potential at origin
Now, if another charge
By putting the value of
or






