Electrostatics 2 Question 27
28. Two fixed charges $-2 Q$ and $Q$ are located at the points with coordinates $(-3 a, 0)$ and $(+3 a, 0)$ respectively in the $x-y$ plane.
(1991, 8M)
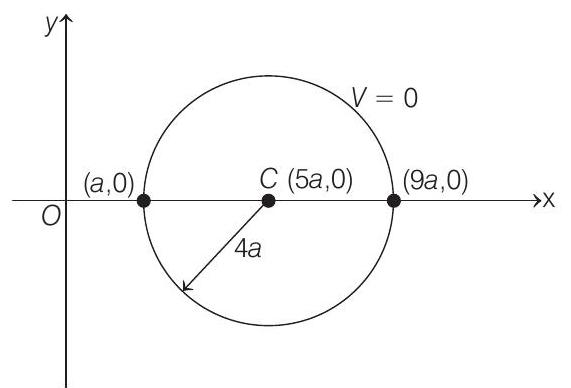
(a) Show that all points in the $x-y$ plane where the electric potential due to the two charges is zero, lie on a circle. Find its radius and the location of its centre.
(b) Give the expression $V(x)$ at a general point on the $x$-axis and sketch the function $V(x)$ on the whole $x$-axis.
(c) If a particle of charge $+q$ starts form rest at the centre of the circle, show by a short quantitative argument that the particle eventually crosses the circle. Find its speed when it does so.
Show Answer
Solution:
- (a) Let $P(x, y)$ be a general point on $x-y$ plane. Electric potential at point $P$ would be,
$V=($ potential due to $Q)+$ (potential due to $-2 Q)$
or
$$ \begin{aligned} & V=\frac{1}{4 \pi \varepsilon _0} \frac{Q}{\sqrt{(3 a-x)^{2}+y^{2}}} \\ & \\ & \quad+\frac{1}{4 \pi \varepsilon _0} \frac{-2 Q}{\sqrt{(3 a+x)^{2}+y^{2}}} \end{aligned} $$
Given $V=0$
$$ \therefore \quad 4\left[(3 a-x)^{2}+y^{2}\right]=(3 a+x)^{2}+y^{2} $$
On simplifying, we get $(x-5 a)^{2}+y^{2}=(4 a)^{2}$
This is the equation of a circle of radius $4 a$ and centre at $(5 a, 0)$.
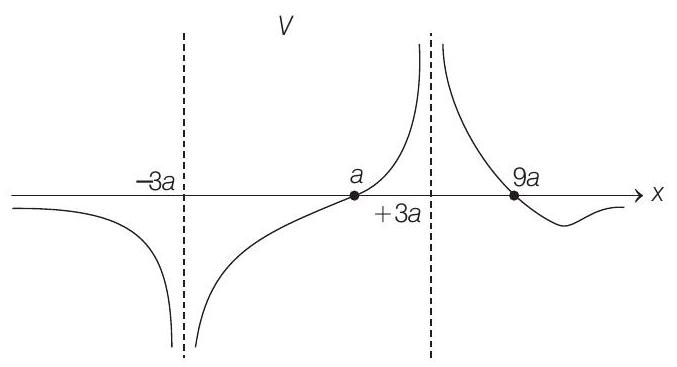
(b) On $x$-axis, potential will be undefined (or say $\pm \infty$ ) at $x=3 a$ and $x=-3 a$, because charge $Q$ and $-2 Q$ are placed at these two points.
So, between $-3 a<x<3 a$ we can find potential by putting $y=0$ in Eq. (i). Therefore,
$$ \begin{gathered} V=\frac{Q}{4 \pi \varepsilon _0} \frac{1}{3 a-x}-\frac{2}{3 a+x} \text { for }-3 a<x<3 a \\ V=0 \text { at } x=a \\ V \rightarrow-\infty \text { at } x \rightarrow-3 a \\ \text { and } \quad V \rightarrow+\infty \text { at } x \rightarrow 3 a \end{gathered} $$
For $x>3 a$, there is again a point where potential will become zero so for $x>3 a$, we can write
$$ \begin{aligned} & V=\frac{Q}{4 \pi \varepsilon _0} \frac{1}{x-3 a}-\frac{2}{3 a+x} \text { for } x>3 a \\ & V=0 \text { at } x=9 a \end{aligned} $$
For $x<-3 a$, we can write
$$ V=\frac{Q}{4 \pi \varepsilon _0} \frac{1}{3 a-x}-\frac{2}{3 a-x} \text { for } x<-3 a $$
In this region potential will be zero only at $x \rightarrow-\infty$ Thus, we can summarise it as under.
(i) At $x=3 a, V=+\infty$
(ii) At $x=-3 a, V=-\infty$
(iii) For $x<-3 a, V=\frac{Q}{4 \pi \varepsilon _0} \frac{1}{3 a-x}-\frac{2}{3 a+x}$
(iv) For $-3 a<x<3 a$, expression of $V$ is same i.e.
$$ V=\frac{Q}{4 \pi \varepsilon _0} \frac{1}{3 a-x}-\frac{2}{3 a+x} $$
(v) For $x>3 a, V=\frac{Q}{4 \pi \varepsilon _0} \frac{1}{x-3 a}-\frac{2}{3 a+x}$
Potential on $x$-axis is zero at two places at $x=a$ and $x=9 a$.
The $V-x$ graph is shown below,
Exercise (i) Find potential at $x=0$.
(ii) In the graph for $x>9 a$, find where $|V|$ will be maximum and what will be its value?
(c) Potential at centre i.e. at $x=5 a$ will be,
$$ V=\frac{Q}{4 \pi \varepsilon _0} \frac{1}{2 a}-\frac{2}{8 a}=\frac{Q}{16 \pi \varepsilon _0 a}=\text { positive } $$
Potential on the circle will be zero.
Since, potential at centre $>$ potential on circumference on it, the particle will cross the circle because positive charge moves from higher potential to lower potential. Speed of particle, while crossing the circle would be,
$$ v=\sqrt{\frac{2 q(\Delta V)}{m}}=\sqrt{\frac{Q q}{8 \pi \varepsilon _0 m a}} $$
Here, $\Delta V$ is the potential difference between the centre and circumference of the circle.






