Electrostatics 2 Question 2
2. A system of three charges are placed as shown in the figure
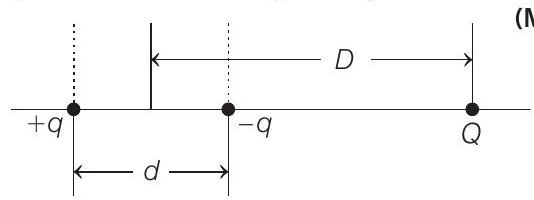
(Main 2019, 9 April I)
If
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- The system of two charges, i.e.
So, the total potential energy of the system will be due to two components.
(1) Potential energy of dipole’s own system
(2) Potential energy of charge
Hence, total potential energy of the system






