Electrostatics 1 Question 4
4. Charge is distributed within a sphere of radius $R$ with a volume charge density $\rho(r)=\frac{A}{r^{2}} e^{\frac{-2 r}{a}}$, where $A$ and $a$ are constants. If $Q$ is the total charge of this charge distribution, the radius $R$ is
(Main 2019, 9 Jan Shift II)
(a) $a \log \frac{1}{1-\frac{Q}{2 \pi a A}}$
(b) $a \log 1-\frac{Q}{2 \pi a A}$
(c) $\frac{a}{2} \log 1-\frac{Q}{2 \pi a A}$
(d) $\frac{a}{2} \log \frac{1}{1-\frac{Q}{2 \pi a A}}$
Show Answer
Answer:
Correct Answer: 4. (c)
Solution:
- Here, volume charge density,
$$ \rho(r)=\frac{A}{r^{2}} \cdot e^{-\frac{2 r}{a}} $$
where, $a$ and $A$ are constant.
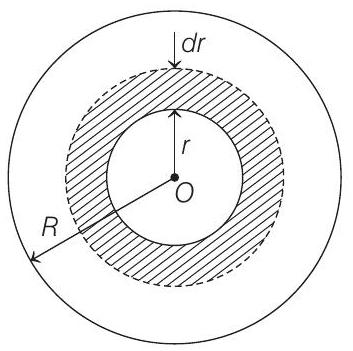
Let a spherical region of small element of radius $r$. If $Q$ is total charge distribution upto radius $R$, then
$$ Q=\int _0^{R} \rho \cdot d V=\int _0^{R} \frac{A}{r^{2}} e^{-2 r / a}\left(4 \pi r^{2} d r\right) $$
(From figure, we observe $d V=A \cdot d r=4 \pi r^{2} \cdot d r$ )
$$ \begin{aligned} & =4 \pi A \int _0^{R} e^{-2 r / a} d r=4 \pi A{\frac{e^{-2 r / a}}{-2 / a}} _0^{R} \\ & =4 \pi A \times \frac{-a}{2}\left(e^{-2 R / a}-e^{0}\right) \\ & =2 \pi A(-a)\left[e^{-2 R / a}-1\right] \\ \text { or } \quad Q & =2 \pi a A\left(1-e^{-2 R / a}\right) \\ \text { or } \quad R & =\frac{a}{2} \log \frac{1}{1-\frac{Q}{2 \pi a A}} \end{aligned} $$






