Electrostatics 1 Question 17
18. An infinitely long solid cylinder of radius
The value of
(2012)
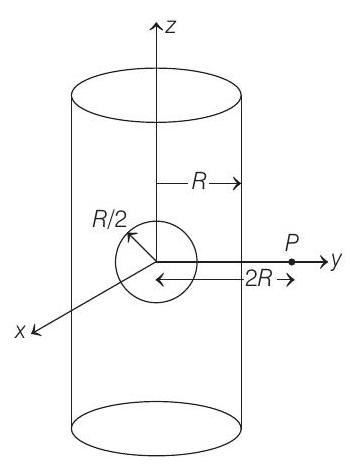
Show Answer
Answer:
Correct Answer: 18. (b)
Solution:
- Volume of cylinder per unit length
Now at
Substituting the values, we have






