Electromagnetic Induction and Alternating Current 7 Question 6
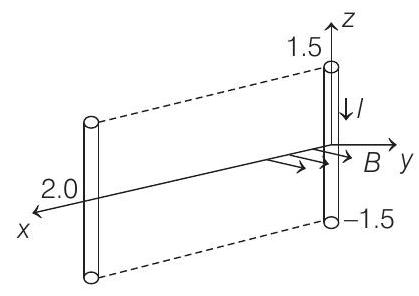
6. A conductor lies along the z-axis at $-1.5 \leq z<1.5 m$ and carries a fixed current of 10.0 $A$ in $-a _z$ direction (see figure). For a field $\mathbf{B}=3.0 \times 10^{-4} e^{-0.2 x} a _y T$, find the power required to move the conductor at constant speed to $x=2.0 m, y=0$ in $5 \times 10^{-3} s$.
Assume parallel motion along the $x$-axis.
(2014 Main)
(a) $1.57 W$
(b) $2.97 W$
(c) $14.85 W$
(d) $29.7 W$
Show Answer
Answer:
Correct Answer: 6. (b)
Solution:
- When force exerted on a current carrying conductor
$$ F _{ext}=B I L $$
Average power $=\frac{\text { Work done }}{\text { Time taken }}$
$$ \begin{aligned} P & =\frac{1}{t} \int _0^{2} F _{\text {ext. }} \cdot d x=\frac{1}{t} \int _0^{2} B(x) I L d x \\ & =\frac{1}{5 \times 10^{-3}} \int _0^{2} 3 \times 10^{-4} e^{-0.2 x} \times 10 \times 3 d x \\ & =9\left[1-e^{-0.4}\right]=91-\frac{1}{e^{0.4}} \\ & =2.967 \approx 2.97 W \end{aligned} $$
