Electromagnetic Induction and Alternating Current 7 Question 29
####32. Two long parallel horizontal rails, a distance $d$ apart and each having a resistance $\lambda$ per unit length, are joined at one end by a resistance $R$. A perfectly conducting $\operatorname{rod} M N$ of mass $m$ is free to slide
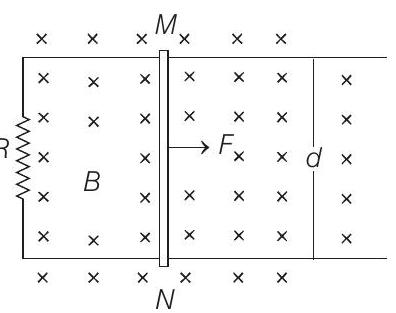along the rails without friction (see figure). There is a uniform magnetic field of induction $B$ normal to the plane of the paper and directed into the paper. A variable force $F$ is applied to the $\operatorname{rod} M N$ such that, as the rod moves, a constant current $i$ flows through $R$.
Find the velocity of the rod and the applied force $F$ as functions of the distance $x$ of the rod from R.v
$(1988,6 M)$
Show Answer
Answer:
Correct Answer: 32. $v=\frac{(R+2 \lambda x) i}{B d}, F=\frac{2 \lambda i^{2} m}{B^{2} d^{2}}(R+2 \lambda x)^{2}+i d B$
Solution:
- Total resistance of the circuit as function of distance $x$ from resistance $R$ is $R _{\text {net }}=R+2 \lambda x$
Let $v$ be velocity of rod at this instant, then motional emf induced across the rod, $e=B v d$
$\therefore \quad$ Current $i=\frac{e}{R _{\text {net }}}=\frac{B v d}{R+2 \lambda x} \Rightarrow v=\frac{(R+2 \lambda x) i}{B d}$
Net force on the rod, $F _{\text {net }}=m \frac{d v}{d t}=\frac{2 \lambda i m}{B d}(R+2 \lambda x) \cdot \frac{d x}{d t}$
but
$$ \begin{aligned} \frac{d x}{d t} & =v=\frac{(R+2 \lambda x) i}{B d} \\ F _{\text {net }} & =\frac{2 \lambda i^{2} m}{B^{2} d^{2}}(R+2 \lambda x)^{2} \end{aligned} $$
This net force is equal to $F-F _m$ where $F _m=i d B$
$\therefore \quad F=F _{\text {net }}+F _m=\frac{2 \lambda i^{2} m}{B^{2} d^{2}}(R+2 \lambda x)^{2}+i d B$
