Electromagnetic Induction and Alternating Current 7 Question 28
31. An infinitesimally small bar magnet of dipole moment
(1997C, 5M)
Show Answer
Answer:
Correct Answer: 31.
Solution:
- Given that
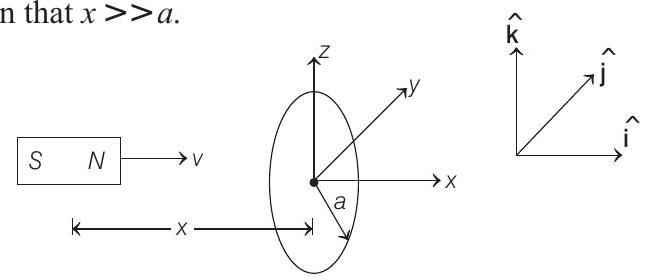
Magnetic field at the centre of the coil due to the bar magnet is
Due to this, magnetic flux linked with the coil will be,
Therefore, induced current in the coil is
Magnetic moment of the coil due to this induced current will be,
Potential energy of
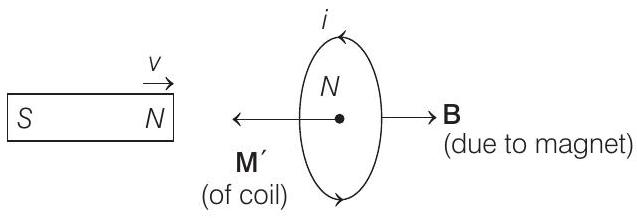
Positive sign of






