Electromagnetic Induction and Alternating Current 7 Question 25
28. A long solenoid of radius $a$ and number of turns per unit length $n$ is enclosed by cylindrical shell of radius $R$, thickness $d(d \ll R)$ and length $L$.
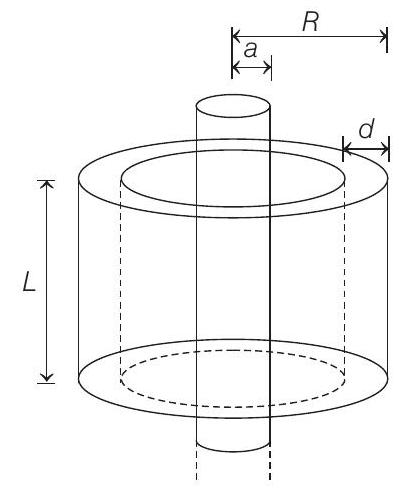
A variable current $i=i _0 \sin \omega t$ flows through the solenoid. If the resistivity of the material of cylindrical shell is $\rho$, find the induced current in the shell.
$(2005,4$ M)
Show Answer
Answer:
Correct Answer: 28. $i=\frac{\mu _0 L d n a^{2} I _0 \omega \cos \omega t}{2 \rho R}$
Solution:
- Outside the solenoid, net magnetic field is zero. It can be assumed only inside the solenoid and equal to $\mu _0 n I$.
Induced $e=-\frac{d \varphi}{d t}=-\frac{d}{d t}\left(\mu _0 n I \pi a^{2}\right)$
or $\quad|e|=\left(\mu _0 n \pi a^{2}\right)\left(I _0 \omega \cos \omega t\right)$
Resistance of the cylindrical vessel, $R=\frac{\rho l}{s}=\frac{\rho(2 \pi R)}{L d}$
$\therefore$ Induced current $i=\frac{|e|}{R}=\frac{\mu _0 L d n a^{2} I _0 \omega \cos \omega t}{2 \rho R}$
