SATHEE: Electromagnetic Induction and Alternating Current 6 Question 3

Electromagnetic Induction and Alternating Current 6 Question 3

3.

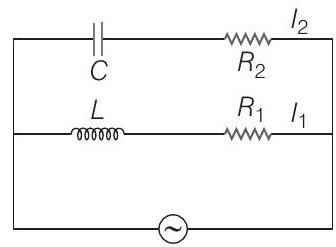
In the above circuit, $C = \frac{\sqrt{3}}{2} μ F, R_{2} = 20 Ω, L = \frac{\sqrt{3}}{10} H$ and $R_{1} = 10 Ω$ . Current in $L - R_{1}$ path is $I_{1}$ and in $C - R_{2}$ path is $I_{2}$ . The voltage of AC source is given by $V = 200 \sqrt{2} \sin (100 t)$ volts. The phase difference between $I_{1}$ and $I_{2}$ is

(a) $30^{\circ}$

(b) $60^{\circ}$

(d) $90^{\circ}$

Show Answer

Answer:

Correct Answer: 3. (a)

Solution:

Phase difference between $I_{2}$ and $V$ , i.e. $C - R_{2}$ circuit is given by

$\tan φ = \frac{X_{C}}{R_{2}} \Rightarrow \tan φ = \frac{1}{C ω R_{2}}$

Substituting the given values, we get

$\tan φ = \frac{1}{\frac{\sqrt{3}}{2} \times 10^{- 6} \times 100 \times 20} = \frac{10^{3}}{\sqrt{3}}$

$∴ φ_{1}$ , is nearly $90^{\circ}$ .

Phase difference between $I_{1}$ and $V$ , i.e. in $L - R_{1}$ circuit is given by

$\tan φ_{2} = - \frac{X_{L}}{R_{1}} = - \frac{L ω}{R}$

Substituting the given values, we get

$\tan φ_{2} = - \frac{\frac{\sqrt{3}}{10} \times 100}{10} = - \sqrt{3}$

As, $\tan φ_{2} = - \sqrt{3} \Rightarrow φ_{2} = 120^{\circ}$

Now, phase difference between $I_{1}$ and $I_{2}$ is

$Δ φ = φ_{2} - φ_{1} = 120^{\circ} - 90^{\circ} = 30^{\circ}$

पिछला

अगला

Electromagnetic Induction and Alternating Current 6 Question 3

3.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Electromagnetic Induction and Alternating Current 6 Question 3

3.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu