Electromagnetic Induction and Alternating Current 6 Question 11
11. In the given circuit, the
(2012)
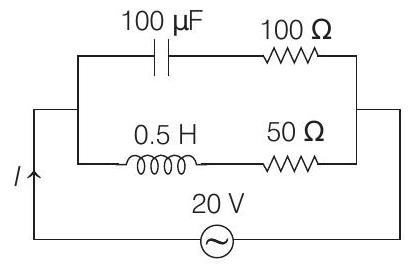
(a) the current through the circuit,
(b) the current through the circuit,
(c) the voltage across
(d) the voltage across
Show Answer
Answer:
Correct Answer: 11.
Solution:
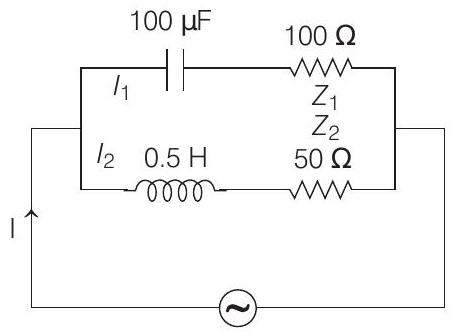
Circuit 1
In this circuit, current leads the voltage.
Circuit 2
In this circuit, voltage leads the current.
Further,






