Electromagnetic Induction and Alternating Current 6 Question 10
10. At time
(2014 Adv.)

(a) Magnitude of the maximum charge on the capacitor before
(b) The current in the left part of the circuit just before
(c) Immediately after
(d)
Show Answer
Answer:
Correct Answer: 10. (c, d)
Solution:
Just after switching

In steady state

At
Current comes out to be negative from the given expression. So, current is anti-clockwise. Charge supplied by source from
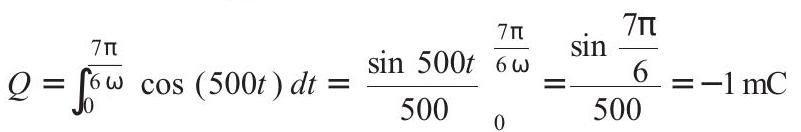
Apply Kirchhoff’s loop law, just after changing the switch to position
Substituting the values of
In steady state






