SATHEE: Electromagnetic Induction and Alternating Current 4 Question 7

Electromagnetic Induction and Alternating Current 4 Question 7

7. An inductor $(L = 0.03 H)$ and a resistor $(R = 0.15 k Ω)$ are connected in series to a battery of $15 V$ EMF in a circuit shown below. The key $K_{1}$ has been kept closed for a long time. Then at $t = 0, K_{1}$ is opened and key $K_{2}$ is closed simultaneously. At $t = 1 m s$ , the current in the circuit will be $(e^{5} ≅ 150)$

(2015 Main)

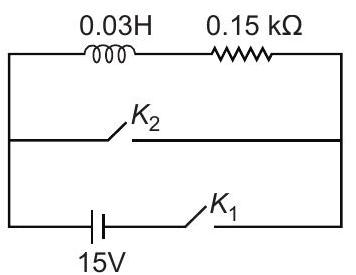
(a) $100 m A$

(b) $67 m A$

(d) $6.7 m A$

Show Answer

Answer:

Correct Answer: 7. (c)

Solution:

Steady state current $i_{0}$ was already flowing in the $L - R$ circuit when $K_{1}$ was closed for a long time. Here,

$i_{0} = \frac{V}{R} = \frac{15 V}{150 Ω} = 0.1 A$

Now, $K_{1}$ is opened and $K_{2}$ is closed. Therefore, this $i_{0}$ will decrease exponentially in the $L - R$ circuit. Current $i$ at time $t$ will be given by $i = i_{0} e^{\frac{- t}{τ_{L}}}$

where, $τ_{L} = \frac{L}{R} \Rightarrow ∴ i = i_{0} e^{\frac{- R t}{L}}$

Substituting the values, we have

$i = (0.1) e^{\frac{- (0.15 \times 10^{3}) (10^{- 3})}{(0.03)}}$

$\begin{aligned} = (0.1) (e^{- 5}) = \frac{0.1}{150} = 6.67 \times 10^{- 4} A \\ = 0.67 m A \end{aligned}$

पिछला

अगला

Electromagnetic Induction and Alternating Current 4 Question 7

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Electromagnetic Induction and Alternating Current 4 Question 7

7. An inductor (L=0.03H) and a resistor (R=0.15kΩ) are connected in series to a battery of 15V EMF in a circuit shown below. The key K1 has been kept closed for a long time. Then at t=0,K1 is opened and key K2 is closed simultaneously. At t=1ms, the current in the circuit will be (e5≅150)

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu