Electromagnetic Induction and Alternating Current 4 Question 5
5. A series $AC$ circuit containing an inductor $(20 mH)$, a capacitor $(120 \mu F)$ and a resistor $(60 \Omega)$ is driven by an $AC$ source of $24 V / 50 Hz$. The energy dissipated in the circuit in $60 s$ is
(Main 2019, 9 Jan II)
(a) $3.39 \times 10^{3} J$
(b) $5.65 \times 10^{2} J$
(c) $2.26 \times 10^{3} J$
(d) $5.17 \times 10^{2} J$
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
- The given series $R-L-C$ circuit is shown in the figure below.
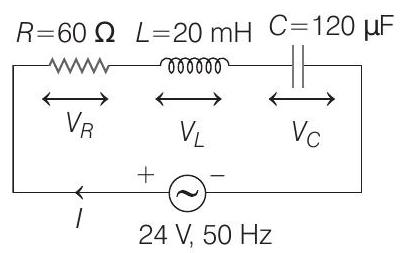
Here,
$V _R=$ potential across resistance $(R)$
$V _L=$ potential across inductor $(L)$ and
$V _C=$ potential across capacitor $(C)$
Impedance of this series circuit is
$$ \begin{aligned} Z & =\sqrt{R^{2}+\left(X _L-X _C\right)^{2}} \\ \because \quad X _L & =\omega L=(2 \pi f)(L) \\ & =2 \pi \times 50 \times 20 \times 10^{-3} \Omega \\ X _L & =6.28 \Omega \\ X _C & =\frac{1}{\omega C}=\frac{1}{2 \pi f C} \\ & =\frac{1}{2 \pi \times 50 \times 120 \times 10^{-6}}=\frac{250}{3 \pi} \Omega \\ \text { and } \quad X _L-X _C & =6.28-\frac{250}{3 \pi}=-20.23 \Omega \end{aligned} $$
RMS value of current in circuit is
$$ \begin{aligned} & I _{rms}=\frac{V _{rms}}{Z}=\frac{24}{\sqrt{R^{2}+\left(X _L-X _C\right)^{2}}} \\ & I _{rms}=\frac{24}{\sqrt{60^{2}+(-20.23)^{2}}}=\frac{24}{63.18} \\ & I _{rms}=0.379 A \end{aligned} $$
Therefore, energy dissipated is
$$ \begin{aligned} & =I _{rms}^{2} \times R \times t \\ E & =(0.379)^{2} \times 60 \times 60 \\ & =517.10=5.17 \times 10^{2} J \end{aligned} $$
