SATHEE: Electromagnetic Induction and Alternating Current 2 Question 9

Electromagnetic Induction and Alternating Current 2 Question 9

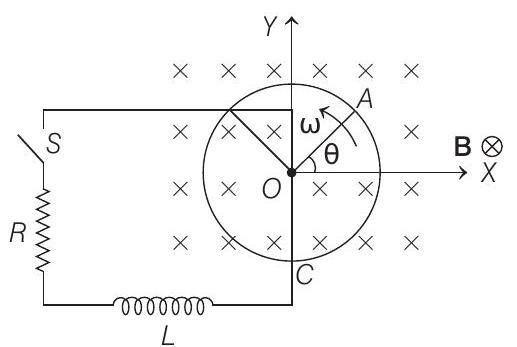10. A metal $rod O A$ and mass $m$ and length $r$ kept rotating with a constant angular speed $ω$ in a vertical plane about horizontal axis at the end $O$ . The free end $A$ is arranged to slide

without friction along a fixed conducting circular ring in the same plane as that of rotation. A uniform and constant magnetic induction $B$ is applied perpendicular and into the plane of rotation as shown in figure. An inductor $L$ and an external resistance $R$ are connected through a switch $S$ between the point $O$ and a point $C$ on the ring to form an electrical circuit. Neglect the resistance of the ring and the rod. Initially, the switch is open.

$(1995, 10 M)$

(a) What is the induced emf across the terminals of the switch?

(b) The switch $S$ is closed at time $t = 0$ .

(i) Obtain an expression for the current as a function of time.

(ii) In the steady state, obtain the time dependence of the torque required to maintain the constant angular speed. Given that the $rod O A$ was along the positive $x$ -axis at $t = 0$ .

Show Answer

Answer:

Correct Answer: 10. (a) $e = \frac{B ω r^{2}}{2}$

(b) (i) $i = \frac{B ω r^{2}}{2 R} 1 - e^{- \frac{R}{L} t}$ (ii) $τ_{net} = \frac{B^{2} ω r^{4}}{4 R} + \frac{m g r}{2} \cos ω t$

Solution:

(a) Consider a small element of length $d x$ of the $rod O A$ situated at a distance $x$ from $O$ .

Speed of this element, $v = x ω$

Therefore, induced emf developed across this element in uniform magnetic field $B$

$d e = (B) (x ω) d x$

$(∵ e = B v l)$

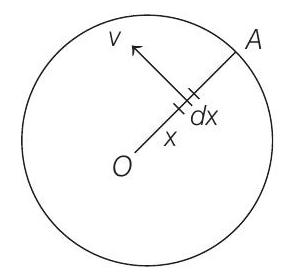
Hence, total induced emf across $O A$ ,

$e = \int_{x = 0}^{x = r} d e = \int_{0}^{r} B ω x d x = \frac{B ω r^{2}}{2} \Rightarrow e = \frac{B ω r^{2}}{2}$

(b) (i) A constant emf or PD, $e = \frac{B ω r^{2}}{2}$ is induced across $O$ and $A$ .

The equivalent circuit can be drawn as shown in the figure.

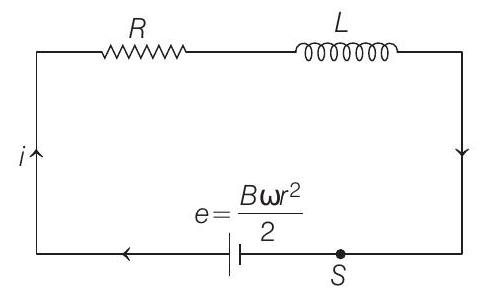
Switch $S$ is closed at time $t = 0$ . Therefore, it is case of growth of current in an $L - R$ circuit. Current at any time $t$ is given by

$\begin{aligned} i & = i_{0} (1 - e^{- t / τ_{L}}), i_{0} = \frac{e}{R} = \frac{B ω r^{2}}{2 R} \\ τ_{L} & = L / R \\ i & = \frac{B ω r^{2}}{2 R} 1 - e^{- \frac{R}{L} t} \end{aligned}$

The $i - t$ graph will be as follows

(ii) At constant angular speed, net torque $= 0$

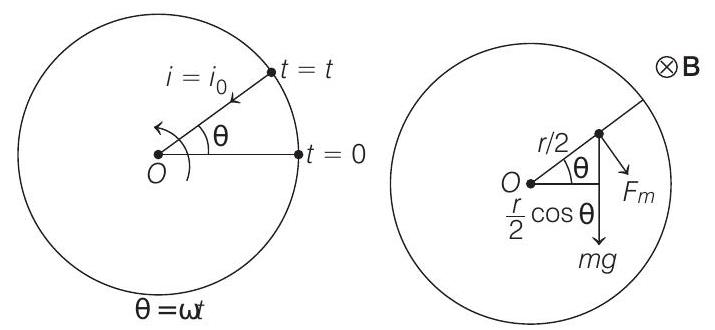
The steady state current will be $i = i_{0} = \frac{B ω r^{2}}{2 R}$

From right hand rule, we can see that this current would be inwards (from circumference to centre) and corresponding magnetic force $F_{m}$ will be in the direction shown in figure and its magnitude is given by

$F_{m} = (i) (r) (B) = \frac{B^{2} ω r^{3}}{2 R}$

$(∵ F_{m} = i l B)$

Torque of this force about centre $O$ is

$τ_{F_{m}} = F_{m} \cdot \frac{r}{2} = \frac{B^{2} ω_{r}^{4}}{4 R}$

(clockwise)

Similarly, torque of weight $(m g)$ about centre $O$ is

$τ_{m g} = (m g) \frac{r}{2} \cos θ = \frac{m g r}{2} \cos ω t (clockwise)$

Therefore, net torque at any time $t$ ( after steady state condition is achieved) about centre $O$ will be

$\begin{aligned} τ_{n e t} & = τ_{F_{m}} + τ_{m g} \\ = \frac{B^{2} ω r^{4}}{4 R} + \frac{m g r}{2} \cos ω t \end{aligned}$

(clockwise)

Hence, the external torque applied to maintain a constant angular speed is $τ_{e x t} = \frac{B^{2} ω r^{4}}{4 R} + \frac{m g r}{2} \cos ω t$ (but in anti-clockwise direction).

Note that for $\frac{π}{2} < θ < \frac{3 π}{2}$ , torque of weight will be anti-clockwise, the sign of which is automatically adjusted because $\cos θ =$ negative for $\frac{π}{2} < θ < \frac{3 π}{2}$ .