Electromagnetic Induction and Alternating Current 2 Question 7
####8. A magnetic field $B=\left(B _0 y / a\right) \hat{\mathbf{k}}$ is acting into the paper in the $+z$ direction. $B _0$ and $a$ are positive constants. A square loop $E F G H$ of side $a$, mass $m$ and resistance $R$ in $x-y$ plane starts falling under the influence of gravity. Note the directions of $x$ and $y$ in the figure. Find
(1999, 10M)
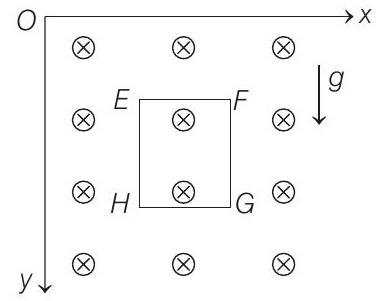
(a) the induced current in the loop and indicate its direction.
(b) the total Lorentz force acting on the loop and indicate its direction.
(c) an expression for the speed of the loop $v(t)$ and its terminal velocity.
Show Answer
Answer:
Correct Answer: 8. (a) $i=\frac{B _0 a v}{R}$, anti-clockwise
(b) $\mathbf{F}=-\frac{B _0^{2} a^{2} v}{R} \hat{\mathbf{j}}$
(c) $v=\frac{g}{K}\left(1-e^{-k T}\right)$, where $K=\frac{B _0^{2} a^{2}}{m R}, v _t=\frac{g}{K}=\frac{g m R}{B _0^{2} a^{2}}$
Solution:
- When the side $E F$ is at a distance $y$ from the $X$-axis, magnetic flux passing through the loop is
$$ \begin{aligned} & \varphi=\int d \varphi=\int _{Y=y}^{Y=y+a} \frac{B _0 Y}{a}(a d Y) \\ & \varphi=\frac{B _0}{2}\left[(y+a)^{2}-y^{2}\right] \end{aligned} $$
(a) Induced emf is
$$ \begin{aligned} & e=\frac{-d \varphi}{d t}=-\frac{B _0}{2}[2(y+a)-2 y] \frac{d y}{d t} \\ & e=B _0 a \frac{d y}{d t} \Rightarrow e=B _0 v a \end{aligned} $$
where, $v=\frac{d y}{d t}=$ speed of loop
$\therefore$ Induced current, $i=\frac{e}{R}=\frac{B _0 a v}{R}$
Direction $|\mathbf{B}| \propto y$ i.e. as the loop comes down $\otimes$ magnetic field passing through the loop increases, therefore the induced current will producer $u$, magnetic field or the induced current in the loop will be counter-clockwise.
Alternate solution (of part a)
Motional emf in $E H$ and $F G=0$ as $\mathbf{v} | \mathbf{I}$
Motional emf in $E F$ is $e _1=\frac{B _0 y}{a}(a) v=B _0 y v \quad(\because e=B l v)$
Similarly, motional emf in $G H$ will be
$$ e _2=\frac{B _0(y+a)}{a}(a)(v)=B _0(a+y) v $$
Polarities of $e _1$ and $e _2$ are shown in adjoining figures.
$$ \begin{array}{ll} \text { Net emf, } & e=e _2-e _1 \\ \therefore & e=B _0 a v \\ \therefore & i=\frac{e}{R}=\frac{B _0 a v}{R} \end{array} $$
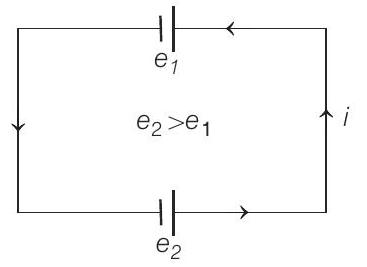
and direction of current will be counter-clockwise.
(b) Total Lorentz force on the loop : $\mathbf{3}$
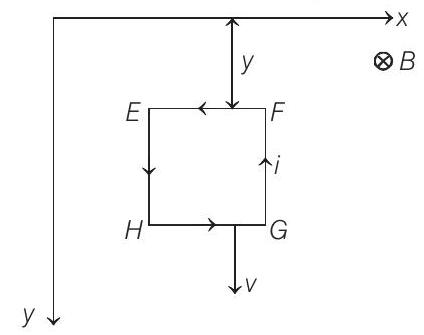
We have seen in part (a) that induced current passing through the loop (when its speed is $v$ ) is
$$ i=\frac{B _0 a v}{R} $$
Now, magnetic force on $E H$ and $F G$ are equal in magnitude and in opposite directions, hence they cancel each other and produce no force on the loop.
$$ \begin{aligned} F _{E F} & =\frac{B _0 a v}{R}(a) \frac{B _0 y}{a} \\ (F & =i l B)=\frac{B _0{ }^{2} a v y}{R} \\ \text { and } \quad F _{G H} & =\frac{B _0 a v}{R}(a) \frac{B _0(y+a)}{a} \\ & =\frac{B _0{ }^{2} a v}{R}(y+a) \\ F _{G H} & >F _{E F} \end{aligned} $$
$\therefore \quad$ Net Lorentz force on the loop
$$ \begin{aligned} \mathbf{F} & =F _{G H}-F _{E F}=\frac{B _0^{2} a^{2} v}{R} \\ \mathbf{F} & =-\frac{B _0^{2} a^{2} v}{R} \hat{\mathbf{j}} \end{aligned} $$
(upwards)
(c) Net force on the loop will be
$F$ = weight - Lorentz force(downwards)
$$ \text { or } \quad \begin{array}{rlrl} F & =m g-\frac{B _0^{2} a^{2} v}{R} \\ \text { or } \quad m \frac{d v}{d t} & =m g-\frac{B _0^{2} a^{2}}{R} v \\ \therefore \quad & \frac{d v}{d t} & =g-\frac{B _0^{2} a^{2}}{m R} v=g-K v \end{array} $$
where, $K=\frac{B _0^{2} a^{2}}{m R}=$ constant
$$ \text { or } \quad \frac{d v}{g-K v}=d t $$
or
$$ \int _0^{v} \frac{d v}{g-K v}=\int _0^{t} d t $$
This equation gives $v=\frac{g}{K}\left(1-e^{-K t}\right)$
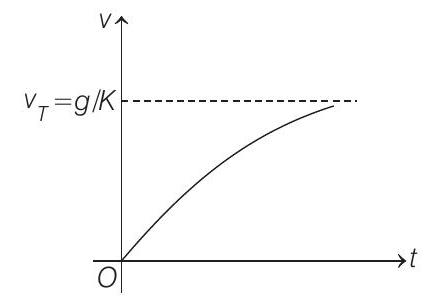
Here, $\quad K=\frac{B _0^{2} a^{2}}{m R}$
i.e. speed of the loop is increasing exponentially with time $t$. Its terminal velocity will be
$$ v _T=\frac{g}{K}=\frac{m g R}{B _0^{2} a^{2}} $$
at $t \rightarrow \infty$
