Electromagnetic Induction and Alternating Current 2 Question 11
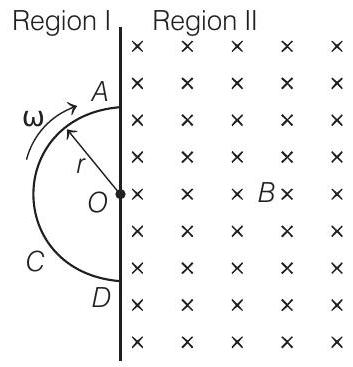
12. Space is divided by the line
The loop is now made to rotate with a constant angular velocity
(a) Obtain an expression for the magnitude of the induced current in the loop.
(b) Show the direction of the current when the loop is entering into the region II.
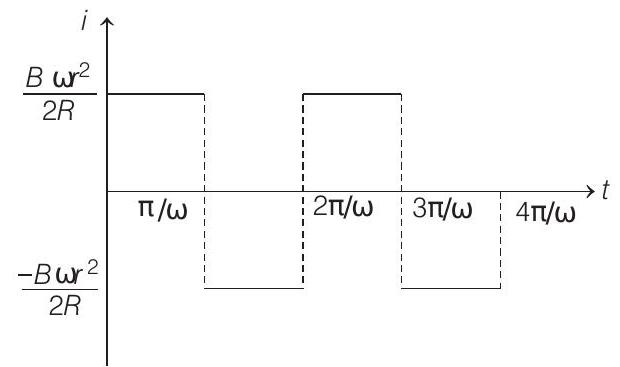
(c) Plot a graph between the induced current and the time of rotation for two periods of rotation.
Show Answer
Answer:
Correct Answer: 12. (a)
Solution:
- (a) At time
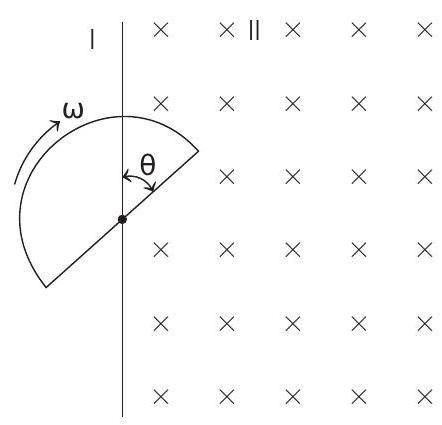
Magnitude of induced emf
(b) When the loop enters in region II, magnetic field in cross direction passing through the loop is increasing. Hence, from the Lenz’s law, induced current will produce magnetic field in dot direction or the current will be anti-clockwise.
(c) For half rotation