Electromagnetic Induction and Alternating Current 1 Question 9
####9. A circular insulated copper wire loop is twisted to form two loops of area $A$ and $2 A$ as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane (of the paper). A uniform magnetic field $\mathbf{B}$ points into the plane of the paper. At $t=0$, the loop starts rotating about the common diameter as axis with a constant angular velocity $\omega$ in the magnetic field. Which of the following options is/are correct?
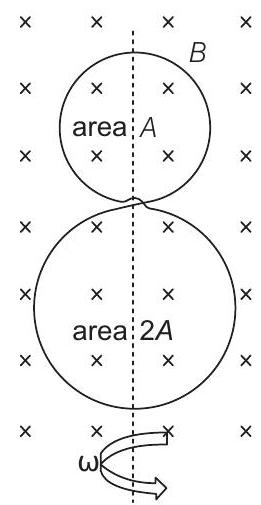
(a) The emf induced in the loop is proportional to the sum of the areas of the two loops.
(b) The rate of change of the flux is maximum when the plane of the loops is perpendicular to plane of the paper.
(c) The net emf induced due to both the loops is proportional to $\cos \omega t$.
(d) The amplitude of the maximum net emf induced due to both the loops is equal to the amplitude of maximum emf induced in the smaller loop alone.
Show Answer
Answer:
Correct Answer: 9. $(b, d)$
Solution:
- The net magnetic flux through the loops at time $t$ is
$$ \varphi=B(2 A-A) \cos \omega t=B A \cos \omega t $$
So, $\frac{d \varphi}{d t}=B \omega A \sin \omega t$
$\therefore \frac{d \varphi}{d t}$ is maximum when $\varphi=\omega t=\pi / 2$
The emf induced in the smaller loop,
$\varepsilon _{\text {smaller }}=-\frac{d}{d t}(B A \cos \omega t)=B \omega A \sin \omega t$
$\therefore$ Amplitude of maximum net emf induced in both the loops
$=$ Amplitude of maximum emf induced in the smaller loop alone.
