Electromagnetic Induction and Alternating Current 1 Question 4
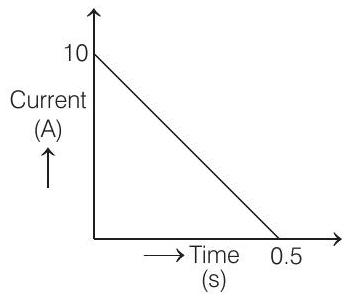
4. In a coil of resistance $100 \Omega$, a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is (2017 Main)
(a) $225 Wb$
(b) $250 Wb$
(c) $275 Wb$
(d) $200 Wb$
Show Answer
Answer:
Correct Answer: 4. (b)
Solution:
- Induced constant, $I=\frac{e}{R}$
Here, $e=$ induced emf $=\frac{d \varphi}{d t}$
$$ \begin{aligned} I & =\frac{1}{R}=\frac{d \varphi}{d t} \cdot \frac{1}{R} \\ d \varphi & =I R d t \\ \varphi & =\int I R d t \end{aligned} $$
$\therefore \quad$ Here, $R$ is constant
$\therefore \quad \varphi=R \int I d t$
$$ \begin{aligned} & \int I \cdot d t=\text { Area under } I-t \text { graph } \\ & \quad=\frac{1}{2} \times 10 \times 0.5=2.5 \\ & \therefore \quad \varphi=R \times 2.5=100 \times 2.5=250 \mathrm{Wb.} . \end{aligned} $$
