Current Electricity 5 Question 3
3. The actual value of resistance
(2019 Main, 10 Jan II))

(a)
(b)
(c)
(d)
Show Answer
Solution:
- Measured value of
Actual values of
So, measured value of
Now, let us assume that internal resistance of voltmeter
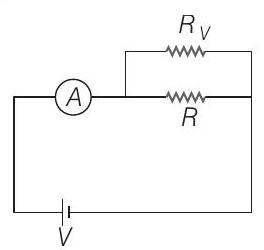
It is clear that the measured value,






