Current Electricity 5 Question 2
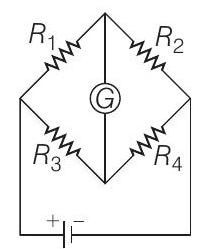
2. The Wheatstone bridge shown in figure here, gets balanced when the carbon resistor is used as $R _1$ has the color code (orange, red, brown). The resistors $R _2$ and $R _4$ are $80 \Omega$ and 40 $\Omega$, respectively.
Assuming that the color code for the carbon resistors gives their accurate values, the color code for the carbon resistor is used as $R _3$ would be
(2019 Main, 10 Jan II)
(a) brown, blue, black
(b) brown, blue, brown
(c) grey, black, brown
(d) red, green, brown
Show Answer
Solution:
- The value of $R _1$ (orange, red, brown)
$$ \Rightarrow \quad=32 \times 10=320 \Omega $$
Given, $R _2=80 \Omega$ and $R _4=40 \Omega$
In balanced Wheatstone bridge condition,
$$ \begin{array}{rlrl} & & \frac{R _1}{R _2}=\frac{R _3}{R _4} \Rightarrow \quad R _3=R _4 \times \frac{R _1}{R _2} \\ \Rightarrow & R _3=\frac{40 \times 320}{80} \\ \text { or } & R _3=160 \Omega=16 \times 10^{1} \end{array} $$
Comparing the value of $R _3$ with the colours assigned for the carbon resistor, we get
$$ \begin{aligned} & R _3=16 \times 10^{1} \\ & \nearrow \uparrow \uparrow \uparrow \uparrow _{\text {Brown Blue Brown }} \end{aligned} $$
